题目内容
【题目】（问题原型）
如图①，AB∥CD，点M在直线AB、CD之间，则∠M＝∠B+∠D，小明解决上述问题的过程如下：
如图②，过点M作MN∥AB
则∠B＝_______（_______）
∵AB∥CD，（已知）
MN∥AB（辅助线的做法）
∴MN∥CD（______）
∴∠______＝∠D（______）
∴∠B+∠D＝∠BMD
请完成小明上面的过程．
（问题迁移）
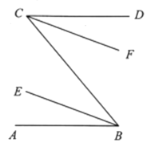
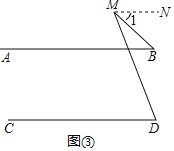
如图③，AB∥CD，点M与直线CD分别在AB的两侧，猜想∠M、∠B、∠D之间有怎样的数量关系，并加以说明．
（推广应用）
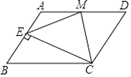
（1）如图④，AB∥CD，点M在直线AB、CD之间，∠ABM的平分线与∠CDM的平分线交于点N，∠M＝96°，则∠N＝_____°；
（2）如图⑤，AB∥CD，点M与直线CD分别在AB的两侧，∠ABM的平分线与∠CDM的平分线交于点N，∠N＝25°，则∠M＝______°；
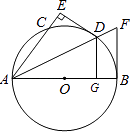
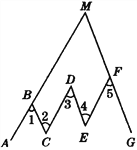
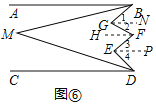
（3）如图⑥，AB∥CD，∠ABG的平分线与∠CDE的平分线交于点M，∠G＝78°，∠F＝64°，∠E＝64°，则∠M＝_______°．
【答案】(问题原型)∠BMN；两直线平行，内错角相等；平行于同一条直线的两直线平行；∠NMD；两直线平行，内错角相等；(问题迁移)∠BMD＝∠D﹣∠B；证明见解析；(推广应用)（1）∠N＝48°；（2）∠M＝50°；（3）∠M＝39°，
【解析】
(问题原型)：过点M作MN∥AB，根据平行线的性质即可得答案；(问题迁移)过点M作MN∥AB，由平行线的性质可得∠1＝∠B，∠NMD＝∠D，利用角的和差即可得答案；(推广应用)：（1）利用图②结论，结合角平分线的性质即可得答案；（2）利用图③的结论，结合角平分线的性质即可得出答案；（3）如图⑥，过G，F，E分别作GN∥AB，FH∥AB，EP∥AB，根据平行线的性质，结合角平分线的性质利用图②的结论即可得出答案.
(问题原型)：
如图②，过点M作MN∥AB，
则∠B＝∠BMN（两直线平行，内错角相等）
∵AB∥CD，（已知）
∴MN∥AB（辅助线的做法）
∴MN∥CD（平行于同一条直线的两直线平行）
∴∠NMD＝∠D（两直线平行，内错角相等）
∴∠B+∠D＝∠BMD，
故答案为：∠BMN，两直线平行，内错角相等，平行于同一条直线的两直线平行，∠NMD，两直线平行，内错角相等，
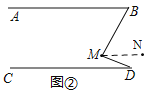
（问题迁移）：
如图③，过点M作MN∥AB，
∴∠1＝∠B，
∵AB∥CD，
∴MN∥AB，
∴∠NMD＝∠D，
∵∠NMD＝∠1+∠BMD，
∴∠BMD＝∠D﹣∠B；
（推广应用）：
（1）如图④，由如图②的结论可得，∠ABM+∠CDM＝∠M＝96°，∠N＝∠ABN+∠CDN，
∵BN，DN分别平分∠ABM，∠CDM，
∴∠ABN+∠CDN＝
＝
（∠ABM+∠CDM）＝48°，
∴∠N＝48°；
（2）如图⑤，由如图③的结论可得，∠M＝∠CDM﹣∠ABM，
∵BN，DN分别平分∠ABM，∠CDM，
∴∠CDN﹣∠ABN＝∠CDM﹣∠ABM＝（∠CDM﹣∠ABM）＝∠M＝∠N＝25°，
∴∠M＝50°；
（3）如图⑥，过G，F，E分别作GN∥AB，FH∥AB，EP∥AB，
∵AB∥CD，
∴AB∥GN∥FH∥EP∥CD，
∴∠2＝∠GFH，∠3＝∠EFH，
∴∠2+∠3＝∠GFE＝64°，
∴∠1+∠4＝∠BGF+∠DEF﹣∠GFE＝78°，
∵AB∥GN，EP∥CD，
∴∠ABG＝∠1，∠CDE＝∠4，
∴∠ABG+∠CDE＝78°，
∵BM，DM分别平分∠ABG，∠CDE，
∴∠ABM＝∠ABG，∠CDM＝∠CDE，
由如图②中的结论可得∠M＝∠ABM+∠CDM＝（∠ABG+∠CDE）＝×78°＝39°，
故答案为：48，50，39．
