Question

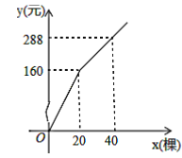
【题目】为更新果树品种，某果园计划新购进、两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中种苗的单价为元/棵，购买种苗所需费用（元）与购买数量（棵）之间存在如图所示的函数关系．

（1）求与的函数关系式；

（2）若在购买计划中，种苗的数量不超过35棵，但不少于种苗的数量，请设计购买方案，使总费用最低，并求出最低费用．

Answer 1

【答案】（1）；（2）购买种树苗23棵总费用最低，（元）．

【解析】

（1）根据题意，待定系数法求得不同范围内函数的解析式即可；

（2）分别计算时对应的费用，即可容易判断.

解：（1）当时，；

当时，设与的函数关系式为：，

把，代入得：，

解得：，∴

综上，．

（2）∵种苗的数量不超过35棵，但不少于种苗的数量，

∴，解得：，

∵为整数，∴，

设总费用为元，则，

若时，，随的增大而减小，

当时，即购买种树苗35棵总费用最低，（元）；

当时，此时为定值，（元）；

当时，，随的增大而增大，

当时，即购买种树苗23棵总费用最低，（元）．