题目内容
四边形ABCD中,∠A:∠B:∠C:∠D=2:1:1:2,则四边形ABCD的形状是
- A.菱形
- B.矩形
- C.等腰梯形
- D.平行四边形
C
分析:由已知条件可知∠A=∠D,∠B=∠C,而由四边形内角和为360°,可推得∠A+∠B=180°,即同旁内角互补,根据等腰梯形的判定可知四边形ABCD的形状是等腰梯形.
解答: 解:∵∠A:∠B:∠C:∠D=2:1:1:2,
解:∵∠A:∠B:∠C:∠D=2:1:1:2,
∴∠A=∠D,∠B=∠C,且∠A≠∠B,∠C≠∠D,
∴2(∠A+∠B)=360°,
∴∠A+∠B=180°,即同旁内角互补;
∴四边形ABCD的形状是等腰梯形.
故选C.
点评:此题考查了等腰梯形的判定方法,需注意的是判定梯形必须满足两个条件:①一组对边平行,②另一组对边不平行,缺一不可.
分析:由已知条件可知∠A=∠D,∠B=∠C,而由四边形内角和为360°,可推得∠A+∠B=180°,即同旁内角互补,根据等腰梯形的判定可知四边形ABCD的形状是等腰梯形.
解答:
 解:∵∠A:∠B:∠C:∠D=2:1:1:2,
解:∵∠A:∠B:∠C:∠D=2:1:1:2,∴∠A=∠D,∠B=∠C,且∠A≠∠B,∠C≠∠D,
∴2(∠A+∠B)=360°,
∴∠A+∠B=180°,即同旁内角互补;
∴四边形ABCD的形状是等腰梯形.
故选C.
点评:此题考查了等腰梯形的判定方法,需注意的是判定梯形必须满足两个条件:①一组对边平行,②另一组对边不平行,缺一不可.

练习册系列答案
相关题目
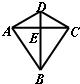 23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.
23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.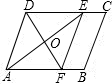 如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( )
如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( )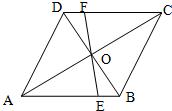 17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形:
17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形: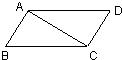 7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.
7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.