题目内容
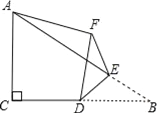
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF的长取最小值时,BF的长为_____.
【答案】![]() .
.
【解析】试题分析::由题意得:DF=DB,
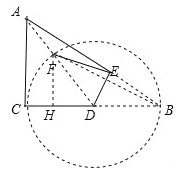
∴点F在以D为圆心,BD为半径的圆上,作⊙D; 连接AD交⊙D于点F,此时AF值最小,
∵点D是边BC的中点,
∴CD=BD=3;而AC=4,
由勾股定理得:AD2=AC2+CD2
∴AD=5,而FD=3,
∴FA=5﹣3=2,
即线段AF长的最小值是2,
连接BF,过F作FH⊥BC于H,
∵∠ACB=90°,
∴FH∥AC,
∴△DFH∽△ADC,
∴![]() ,
,
∴HF=![]() ,DH=
,DH=![]() ,
,
∴BH=![]() ,
,
∴BF=![]() =
=![]() .
.

练习册系列答案
相关题目
【题目】五位学生的一分钟跳绳成绩分布为(单位:个):126,134,134,135,160,在统计数据时,把其中一个134写出了124,则计算结果不受影响的是( )
A.中位数B.众数C.方差D.平均数
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
x | ﹣1 | 0 | 0.5 | 2 |
y | ﹣1 | 2 | 3.75 | 2 |
①ac<0;
②当x>1时,y的值随x值的增大而减小;
③x=2是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<2时,ax2+(b﹣1)x+c>0.
上述结论中正确的有( )个.
A.1 B.2 C.3 D.4