题目内容
【题目】已知:在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是边
是边![]() 上一点.
上一点.
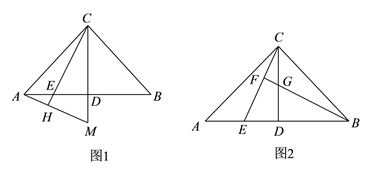
(![]() )如图
)如图![]() ,若
,若![]() 交
交![]() 延长线于点
延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证: ![]() ;
;
(![]() )如图
)如图![]() ,若
,若![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,
, ![]() 的延长线交
的延长线交![]() 于
于![]() ,请判断线段
,请判断线段![]() 与
与![]() 的关系,并证明你的猜想.
的关系,并证明你的猜想.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() 且
且![]() .
.
【解析】试题分析:(1)由等腰直角三角形的性质得到:AD=CD,再证明△MAD≌△ECD,即可得到结论.
(2)(2)证明△ACE≌△CBG,得到CE=BG,∠ACE=∠CBG,再证明BG⊥CE即可.
试题解析:(![]() )证明:∵点D是AB中点,AC=BC,∠ACB=90°,∴CD⊥AB,∠ACD=∠DAC=45°,∴AD=CD.
)证明:∵点D是AB中点,AC=BC,∠ACB=90°,∴CD⊥AB,∠ACD=∠DAC=45°,∴AD=CD.
又∵AH⊥CE,∴∠HAE+∠AEH=90°,
又∵∠CED+∠ECD=90°,∠AEH=∠CED(对顶角相等),∴∠HAE=∠ECD,
在△MAD和△ECD中.∵∠MAD=∠ECD,AD=CD,∠ADM=∠CDE=90°,
∴△MAD≌△ECD(ASA ),∴DE=DM.
(2)BG=CE且BG⊥CE.证明如下:
∵点D是AB中点,AC=BC,∠ACB=90°,∴CD⊥AB,∠CAD=∠BCD=45°.
在△ACE和△CBG中,∵AC=BC,∠CAE=∠BCG=45°,AE=CG,∴△ACE≌△CBG(SAS ),∴CE=BG,∠ACE=∠CBG.
又∵∠ACB=90°,∴∠ACE+∠ECB=90°,∴∠CBG+∠ECB=90°,∴在△BCF中,∠FCB+∠CBF=90°,∴∠CFB=90°,∴BF⊥CE即BG⊥CE,
综上所述,BG=CE且BG⊥CE.

练习册系列答案
相关题目