Question

【题目】二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如表：

x	﹣1	0	0.5	2
y	﹣1	2	3.75	2

①ac＜0；

②当x＞1时，y的值随x值的增大而减小；

③x=2是方程ax2+（b﹣1）x+c=0的一个根；

④当﹣1＜x＜2时，ax2+（b﹣1）x+c＞0．

上述结论中正确的有（ ）个．

A．1 B．2 C．3 D．4

Answer 1

【答案】D

【解析】

试题分析：将（﹣1，﹣1），（0，2）（2，2）代入函数解析时，

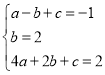得，解得．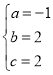

故函数解析式为y=﹣x2+2x+2，

ac=﹣1×2=﹣2＜0，故①正确；

y=﹣x2+2x+2=﹣（x﹣1）2+3，当x＞1时，y的值随x值的增大而减小，故②正确；

﹣x2+x+2=0，解得x=﹣1，x=2，故③正确；

当﹣1＜x＜2时，y=ax2+（b﹣1）x+c的图象位于x轴上方，故④正确；

故选：D．