��Ŀ����
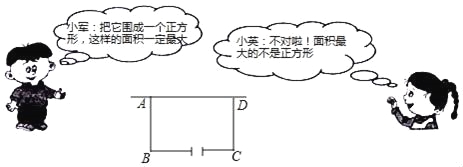
����Ŀ����ͼ,������ABCD��������AEFG��һ��������A����G��E�ֱ����߶�AD��AB�ϣ�
��1������DF��BF������������AEFG�Ƶ�A��˳ʱ�뷽����ת���ж�����������ת�Ĺ����У��߶�DF��BF�ij�ʼ��������Ƿ���ȷ����___________��
��2������������AEFG�Ƶ�A��˳ʱ�뷽����ת������DG������ת�����У����ܷ��ҵ�һ���߶εij����߶�DG�ij�ʼ����ȣ�����ͼΪ��˵�����ɣ�
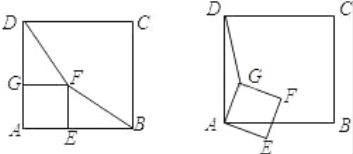
���𰸡�(1)������ȷ��(2)��DG=BE��֤�����̼�����.
��������
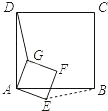
���������(1)�����ݵڶ���ͼ�ξͿ��Եó�DF��BF����ȣ�(2)�����������ε����ʵó�AD=AB��AG=AE����DAG=��BAE���Ӷ��ó���DAG����BAEȫ�ȣ��Ӷ��ó�DG=BE.
���������(1)������ȷ��
(2)��DG=BE
��ͼ�����ı���ABCD�������Σ� ��AD=AB�����ı���GAEF�������Σ���AG=AE��
���ߡ�DAG+��GAB=90������BAE+��GAB=90���� ���DAG=��BAE�� ���DAG�ա�BAE��
��DG=BE��

��ϰ��ϵ�д�
 53���ò�ϵ�д�
53���ò�ϵ�д�
�����Ŀ