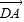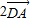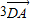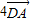题目内容
已知点A、B分别在一次函数y=x,y=8x,的图像上,其横坐标分别为a、b(a>0,b>O).若直线AB为一次函数y=kx+m,的图像,则当![]() 是整数时,满足条件的整数k的值共有 个.
是整数时,满足条件的整数k的值共有 个.
15或9
【解析】
试题分析:依题意知,点A、B分别在一次函数y=x,y=8x,的图像上,其横坐标分别为a、b,则点A坐标为(a,a)B点坐标为(b,8b)。若直线AB为一次函数y=kx+m,的图像,则把A、B坐标代入一次函数解析式中得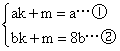 ②-①得:k=
②-①得:k=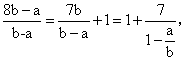
∵a>0,b>0,![]() 是整数时,k也为整数
是整数时,k也为整数
∴![]() 。此时k=15或k=9.
。此时k=15或k=9.
所以满足条件的整数k的值共有两个.
考点:函数解析式
点评:本题难度较大,主要考查待定系数法求函数解析式,解答本题的关键在于对![]() 、k是整数的理解.注意数形结合的应用
、k是整数的理解.注意数形结合的应用

练习册系列答案
相关题目
探索性问题
数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形![]() 结合”的基础。请利用数轴回答下列问题:
结合”的基础。请利用数轴回答下列问题:
已知点A、B在数轴上分别![]() 表示数a、b.
表示数a、b.
(1)填写下表:
| 数 | 列A | 列B | 列C | 列D | 列E | 列F |
| a | 5 | -5 | -6 | -6 | -10 | -2.5 |
| b | 3 | 0 | 4 | -4 | 2 | -2.5 |
| A、B两点的距离 |
(2)任取上表一列数,你发现距离表示可列式为 ,则轴上表示![]() 和
和![]() 的两点之间的距离可表示为 .
的两点之间的距离可表示为 .
(3)若![]() 表示一个有理数,且
表示一个有理数,且![]() ,则
,则![]() = .
= .
(4)若A、B两点的距离为 d,则d与a、b有何数量关系.
 (2013•嘉定区一模)如图,已知点D、E分别在△ABC的边AB和AC上,DE∥BC,AD=
(2013•嘉定区一模)如图,已知点D、E分别在△ABC的边AB和AC上,DE∥BC,AD=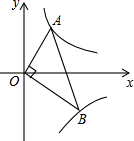 (2013•惠山区一模)已知点A,B分别在反比例函数y=
(2013•惠山区一模)已知点A,B分别在反比例函数y=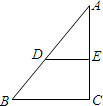 (2013•闸北区一模)如图,已知点D、E分别在△ABC的边AB和AC上,且DE∥BC,S△AED:S梯形EDBC=1:2,则AE:AC的比值是
(2013•闸北区一模)如图,已知点D、E分别在△ABC的边AB和AC上,且DE∥BC,S△AED:S梯形EDBC=1:2,则AE:AC的比值是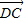 等于( )
等于( )