题目内容
（2013•嘉定区一模）如图，已知点D、E分别在△ABC的边AB和AC上，DE∥BC，AD=| 1 |
| 2 |
（1）求△ABC的面积；
（2）如果向量
| AD |
| a |
| AE |
| b |
| a |
| b |
| BC |
分析：（1）设△ADE的面积为x，则△ABC的面积=x+16，再由△ADE∽△ABC，根据面积比等于相似比平方可得出x的值，继而得出△ABC的面积；
（2）先表示出DE，根据BC=3DE，即可表示出向量
．
（2）先表示出DE，根据BC=3DE，即可表示出向量
| BC |
解答：解：（1）设△ADE的面积为x，则△ABC的面积=x+16，
∵DE∥BC，
∴△ADE∽△ABC，
∴
=（
）2=（
）2，
解得：x=2，
故△ABC的面积为18．
（2）∵向量
=
，向量
=
，
∴
=
-
=
-
，
∵
=
=
，
∴BC=3DE，
∴
=3
-3
．
∵DE∥BC，
∴△ADE∽△ABC，
∴
| x |
| x+16 |
| AD |
| AB |
| 1 |
| 3 |
解得：x=2，
故△ABC的面积为18．
（2）∵向量
| AD |
| a |
| AE |
| b |
∴
. |
| DE |
. |
| AE |
. |
| AD |
. |
| b |
. |
| a |
∵
| DE |
| BC |
| AD |
| AB |
| 1 |
| 3 |
∴BC=3DE，
∴
. |
| BC |
. |
| b |
. |
| a |
点评：本题考查了平面向量及相似三角形的性质，解答本题的关键是掌握相似三角形的面积比等于相似比的平方．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
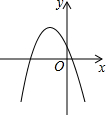（2013•嘉定区一模）已知抛物线y=-x2+bx+c如图所示，那么b、c的取值范围是（ ）