题目内容
【题目】正方形ABCD中，对角线AC，BD相交于点O，DE平分∠ADO交AC于点E，把△ADE沿AD翻折，得到△ADE′，点F是DE的中点，连接AF，BF，E′F．若AE= 
．则四边形ABFE′的面积是 ． 
【答案】
【解析】解：如图，连接EB、EE′，作EM⊥AB于M，EE′交AD于N．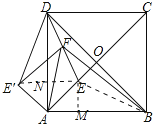
∵四边形ABCD是正方形，
∴AB=BC=CD=DA，AC⊥BD，AO=OB=OD=OC，
∠DAC=∠CAB=∠DAE′=45°，
根据对称性，△ADE≌△ADE′≌△ABE，
∴DE=DE′，AE=AE′，
∴AD垂直平分EE′，
∴EN=NE′，
∵∠NAE=∠NEA=∠MAE=∠MEA=45°，AE= 
，
∴AM=EM=EN=AN=1，
∵ED平分∠ADO，EN⊥DA，EO⊥DB，
∴EN=EO=1，AO= +1，∴AB= AO=2+ ，∴S△AEB=S△AED=S△ADE′= 
×1（2+ ）=1+ 
，S△BDE=S△ADB﹣2S△AEB=1+ ，
∵DF=EF，
∴S△EFB= 
，∴S△DEE′=2S△ADE﹣S△AEE′= +1，S△DFE′= S△DEE′= 
，∴S四边形AEFE′=2S△ADE﹣S△DFE′= 
，∴S四边形ABFE′=S四边形AEFE′+S△AEB+S△EFB= ．
所以答案是 ．
【考点精析】利用正方形的性质和翻折变换（折叠问题）对题目进行判断即可得到答案，需要熟知正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
