题目内容
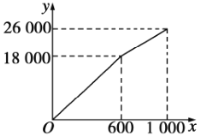
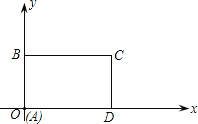
【题目】如图所示,在直角坐标系中,矩形![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() 在原点,
在原点,![]() .若矩形以每秒2个单位长度沿
.若矩形以每秒2个单位长度沿![]() 轴正方向作匀速运动.同时点
轴正方向作匀速运动.同时点![]() 从点
从点![]() 出发以每秒1个单位长度沿
出发以每秒1个单位长度沿![]() 的路线作匀速运动,当
的路线作匀速运动,当![]() 点运动到
点运动到![]() 点时停止运动,矩形
点时停止运动,矩形![]() 也随之停止运动.设
也随之停止运动.设![]() 点运动时间为
点运动时间为![]() (秒).
(秒).
(1)当![]() 时,求出点
时,求出点![]() 的坐标;
的坐标;
(2)若![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 与
与![]() 之间的函数关系式(并写出相应的自变量
之间的函数关系式(并写出相应的自变量![]() 的取值范围).
的取值范围).
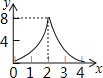
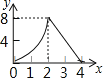
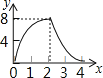
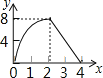
(3)画出题(2)所列的函数的大致图象.
【答案】(1)(12,3);(2)当0<t≤3时,s=t2;当3<t≤8时,s=3t;当8<t<11时,s=-t2+11t;(3)见解析
【解析】
(1)先判断出先P在边BC上,向右移动的单位数,再确定出矩形向右平移的单位数即可得出结论;
(2)分三种情况利用三角形的面积公式即可求解.
(3)在同一平面直角坐标系中分别画出三段函数在相应自变量范围内的图像即可.
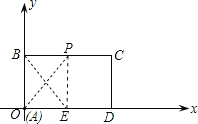
解:(1)当t=5时,P点从A点运动到BC上,
过点P作PE⊥AD于点E.
此时A点到E点的距离=10,AB+BP=5,
∴BP=2
则PE=AB=3,AE=BP=2
∴OE=OA+AE=10+2=12
∴点P的坐标为(12,3);
(2)分三种情况:
①0<t≤3时,点P在AB上运动,此时OA=2t,AP=t
∴s=![]() ×2t×t=t2;
×2t×t=t2;
②3<t≤8时,点P在BC上运动,此时OA=2t
∴s=![]() ×2t×3=3t;
×2t×3=3t;
③8<t<11时,点P在CD上运动,此时OA=2t,AB+BC+CP=t
∴DP=(AB+BC+CD)-(AB+BC+CP)=11-t
∴s=![]() ×2t×(11-t)=-t2+11t;
×2t×(11-t)=-t2+11t;
综上所述,s与t之间的函数关系式是:
当0<t≤3时,s=t2;
当3<t≤8时,s=3t;
当8<t<11时,s=-t2+11t;
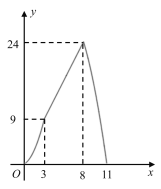
(3)根据(2)中三个函数可得如图:

练习册系列答案
相关题目