题目内容
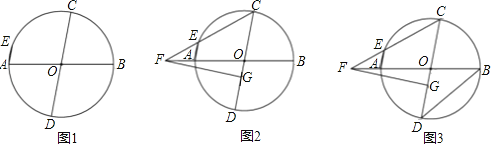
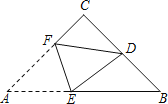
【题目】如图①,![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点,
上一点,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 中点,
中点,![]() 的延长线交
的延长线交![]() 于点
于点![]() .
.
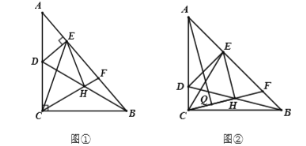
(1)求证;![]() ;
;
(2)若![]() ,求
,求![]() ;
;
(3)如图②,若![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,求证;
,求证;![]() .
.
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)根据直角三角形斜边中线的性质证明即可.
(2)先根据等腰三角形的性质得:∠HCB=∠HBC,∠HEB=∠HBE,由三角形外角的性质得:∠DHC=2∠HBC,∠DHE=2∠HBE,从而有∠CHE=2∠CBA,计算∠CBA=50°,根据平角的定义可得结论;
(3)如图②,连接AH,先证明AE=ED=EH=DH=CH,得△DEH是等边三角形,所以∠DHC=30°,∠AEH=150°,再证明AC=AH,根据等腰三角形三线合一可得AQ⊥CH,最后根据同位角相等,两直线平行可得结论.
(1)证明:∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() ,
,![]() ,
,
∴![]() ;
;
(2)解:如图:
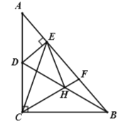
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∴![]()
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)证明;如图,连接![]() ,
,
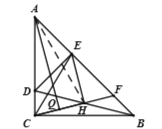
∵![]()
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目