题目内容
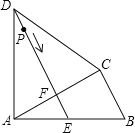
【题目】如图，点D在BC上，AB=AC=BD，AD=DC，则∠BAC的度数是 ．
【答案】108°
【解析】
试题分析：先设∠C=x，由AB=AC可知，∠B=x，由AD=DC可知∠C=∠DAC=x，由三角形外角的性质可知∠ADB=∠C+∠DAC=2x，根据AB=BD可知∠ADB=∠BAD=2x，再在△ABD中，由三角形内角和定理即可得出关于x的一元一次方程，求出x的值即可，然后根据三角形的内角和即可得到结论．
解：设∠C=x，
∵AB=AC，
∴∠C=∠B=x，
∵AD=DC，
∴∠C=∠DAC=x，
∴∠ADB=∠C+∠DAC=2x，
∵AB=BD，
∴∠ADB=∠BAD=2x，
在△ABD中，∠B=x，∠ADB=∠BAD=2x，
∴x+2x+2x=180°，
解得x=36°．
∴∠C=36°，
∴∠BAC=108°，
故答案为：108°．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
