Question

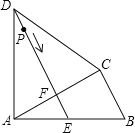
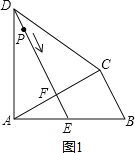
【题目】如图，四边形ABCD中，AD=CD，∠DAB=∠ACB=90°，过点D作DE⊥AC，垂足为F，DE与AB相交于点E．

（1）求证：ABCF=CBCD；

（2）已知AB=15，BC=9，P是射线DE上的动点，设DP=x（x＞0），四边形BCDP的面积为y．

①求y关于x的函数关系式；

②当PB+PC最小时，求x，y的值．

Answer 1

【答案】（1）见解析；（2）①y=（x+9）×6=3x+27（x＞0）；②x=，此时y=．

【解析】

试题分析：（1）首先证得△DCF∽△ABC，利用相似三角形的性质可得结论；

（2）①由勾股定理可得BC的长，利用梯形的面积公式可得结果；②首先由垂直平分线的性质可得点C关于直线DE的对称点是点A，PB+PC=PB+PA，故只要求PB+PA最小即可，因为当P、A、B三点共线时PB+PA最小，由中位线的性质可得EF=，由（1）知CF：BC=CD：AB，可得CD，即得AD，在Rt△ADF中，由勾股定理可得DF，易得DE，即得x，代入①可得y．

（1）证明：如图1，∵AD=CD，DE⊥AC，

∴DE垂直平分AC，

∴AF=CF，∠DFA=∠DFC=90°，∠DAF=∠DCF，

∵∠DAB=∠DAF+∠CAB=90°，∠CAB+∠B=90°，

∴∠DCF=∠DAF=∠B，

在Rt△DCF和Rt△ABC中，∠DFC=∠ACB=90°，∠DCF=∠B，

∴△DCF∽△ABC，

∴，

∴ABCF=CBCD；

（2）解：①∵AB=15，BC=9，∠ACB=90°，

∴AC===12，

∴CF=AF=6，

∴y=（x+9）×6=3x+27（x＞0）；

②由（1）知点C关于直线DE的对称点是点A，

∴PB+PC=PB+PA，故只要求PB+PA最小，显然当P、A、B三点共线时PB+PA最小，

此时DP=DE，PB+PA=AB，

∵EF∥BC，∴EF=，

∵CF：BC=CD：AB，即6：9=CD：15，

∴CD=10=AD，

Rt△ADF中，AD=10，AF=6，

∴DF=8，

∴DE=DF+EF=8+=，

∴x=，此时y=．