题目内容
【题目】阅读下面的学习材料(研学问题)，尝试解决问题：
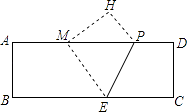
(a)某学习小组在学习时遇到如下问题：如图①，在Rt△ABC中，∠C＝90°，D为边BC上一点，DA＝DB，E为AD延长线上一点，∠AEB＝120°，猜想BC、EA、EB的数量关系，并证明结论．大家经探究发现：过点B作BF⊥AE交AE的延长线于F，如图②所示，构造全等三角形使问题容易求解，请写出解答过程．
(b)参考上述思考问题的方法，解答下列问题：
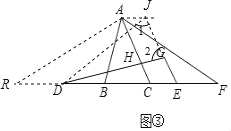
如图③，等腰△ABC中，AB＝AC，H为AC上一点，在BC的延长线上顺次取点E、F，在CB的延长线上取点BD，使EF＝DB，过点E作EG∥AC交DH的延长线于点G，连接AF，若∠HDF+∠F＝∠BAC．
(1)探究∠BAF与∠CHG的数量关系；
(2)请在图中找出一条和线段AF相等的线段，并证明你的结论．
【答案】(a)BC＝AE+
BE．证明见解析；(b)(1)∠CHG＝∠BAF；(2)AF＝DG，证明见解析.
【解析】
（a）如图②中，结论：BC＝AE+BE．理由如下，只要证明△BAF≌△ABC，推出BC＝AF，再证明EF＝BE，可得BC＝AF＝AE+EF＝AE+BE；
（b）（1）由∠F+∠FDG＝∠BAC，推出∠CHG＝∠FDG+∠DCH＝∠FDG+∠F+∠CAF＝∠BAC+∠CAF＝∠BAF；
（2）结论：AF＝DG．如图③中，延长BD到R，使得BR＝CF，连接AR，作AJ∥CF交EG的延长线于J．首先证明四边形ACEJ，四边形AJDR是平行四边形，再证明△ABF≌△JED，想办法证明∠1＝∠2，即可解决问题．
解：(a)如图②中，结论：BC＝AE+BE．理由如下，
∵DA＝DB，
∴∠DBA＝∠DAB，
∵AF⊥BF，
∴∠F＝∠C＝90°，
在△BAF和△ABC中，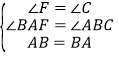
，
∴△BAF≌△ABC(AAS)，
∴BC＝AF，
∵∠AEB＝120°＝∠F+∠FBE，
∴∠FBE＝30°，
∴EF＝BE，
∴BC＝AF＝AE+EF＝AE+BE，
∴BC＝AE+BE；
(b)(1)如图③中，
∵∠HDF+∠F＝∠BAC，
∴∠CHG＝∠FDG+∠DCH＝∠FDG+∠F+∠CAF＝∠BAC+∠CAF＝∠BAF，
∴∠CHG＝∠BAF；
(2)结论：AF＝DG．理由如下，
如图③中，延长BD到R，使得BR＝CF，连接AR，作AJ∥CF交EG的延长线于J，
∵AJ∥CE，AC∥JE，
∴四边形ACEJ是平行四边形，
∴AJ＝CE，AC＝JE，
∵AB＝CA，
∴JE＝AB，
∵AB＝AC，
∴∠ABC＝∠ACB，
∴∠ABR＝∠ACF，
在△ABR和△ACF中，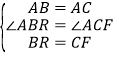
，
∴△ABR≌△ACF(SAS)，
∴AR＝AF，
∵BR＝CF，BD＝EF，
∴DR＝CE＝AJ，ED＝BF，
∵AJ∥RD，
∴四边形ARDJ是平行四边形，
∴JD＝AR＝AF，
在△ABF和△JED中，
，
∴△ABF≌△JED(SSS)，
∴∠1＝∠BAF，
∵∠BAF＝∠CHG＝∠2，
∴∠1＝∠2，
∴DG＝DJ，
∴AF＝DG．
