题目内容
【题目】如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.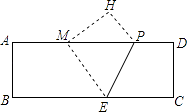
(1)求MP的值;
(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?
(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)
【答案】
(1)解:∵四边形ABCD为矩形,
∴CD=AB=4,∠D=90°,
∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,
∴PD=PH=3,CD=MH=4,∠H=∠D=90°,
∴MP= ![]() =5
=5
(2)解:如图1,作点M关于AB的对称点M′,连接M′E交AB于点F,则点F即为所求,过点E作EN⊥AD,垂足为N,
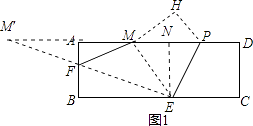
∵AM=AD﹣MP﹣PD=12﹣5﹣3=4,
∴AM=AM′=4,
∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,
∴∠CEP=∠MEP,
而∠CEP=∠MPE,
∴∠MEP=∠MPE,
∴ME=MP=5,
在Rt△ENM中,MN= ![]() =
= ![]() =3,
=3,
∴NM′=11,
∵AF∥NE,
∴△AFM′∽△NEM′,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得AF=
,解得AF= ![]() ,
,
即AF= ![]() 时,△MEF的周长最小
时,△MEF的周长最小
(3)解:如图2,由(2)知点M′是点M关于AB的对称点,在EN上截取ER=2,连接M′R交AB于点G,再过点E作EQ∥RG,交AB于点Q,
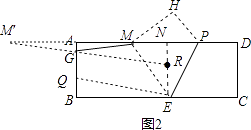
∵ER=GQ,ER∥GQ,
∴四边形ERGQ是平行四边形,
∴QE=GR,
∵GM=GM′,
∴MG+QE=GM′+GR=M′R,此时MG+EQ最小,四边形MEQG的周长最小,
在Rt△M′RN中,NR=4﹣2=2,
M′R= ![]() =5
=5 ![]() ,
,
∵ME=5,GQ=2,
∴四边形MEQG的最小周长值是7+5 ![]() .
.
【解析】(1)根据矩形的性质,四边形ABCD为矩形,得到CD=AB,∠D=90°,再由矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,根据勾股定理得到MP的值;(2)根据折叠的性质,矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,得到∠CEP=∠MEP,ME=MP,根据勾股定理求出MN、NM′的值,由AF∥NE,得到△AFM′∽△NEM′,从而求出AF的值,得到△MEF的周长最小;(3)由(2)知点M′是点M关于AB的对称点,得到四边形ERGQ是平行四边形,得到四边形MEQG的周长最小,根据勾股定理M′R的值,得到四边形MEQG的最小周长值.
【考点精析】本题主要考查了矩形的性质和轴对称-最短路线问题的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径才能正确解答此题.