Question

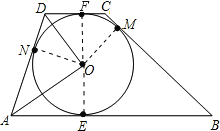
【题目】如图，⊙O是梯形ABCD的内切圆，AB∥DC，E、M、F、N分别是边AB、BC、CD、DA上的切点．

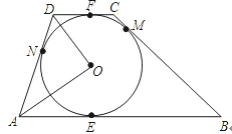
（1）求证：AB+CD=AD+BC

（2）求∠AOD的度数．

Answer 1

【答案】（1）证明见解析；（2）90°.

【解析】

（1）根据切线长定理可证得AE=AN，BE=BM，DF=DN，CF=CM，进而证明AB+DC=AD+BC；

（2）连OE、ON、OM、OF，通过证明△OAE≌△OAN，得到∠OAE=∠OAN．同理：∠ODN=∠ODE，再利用平行线的性质：同旁内角互补即可求出∠AOD的度数．

（1）证明：∵⊙O切梯形ABCD于E、M、F、N，由切线长定理：AE=AN，BE=BM，DF=DN，CF=CM，

∴AE+BE+DF+CF=AN+BM+DN+CM，

∴AB+DC=AD+BC

（2）连OE、ON、OM、OF，

∵OE=ON，AE=AN，OA=OA，

∴△OAE≌△OAN，

∴∠OAE=∠OAN．

同理，∠ODN=∠ODF．

∴∠OAN+∠ODN=∠OAE+∠ODE．

又∵AB∥DC，∠EAN+∠CDN=180°，

∴∠OAN+∠ODN=×180°=90°，

∴∠AOD=180°﹣90°=90°．