题目内容
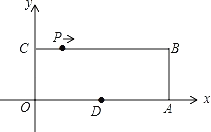
【题目】如图,平面直角坐标系xOy中,点O为坐标原点,四边形OABC为矩形,
A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
(1)直接写出坐标:D( , );
(2)当四边形PODB是平行四边形时,求t的值;
(3)在平面直角坐标系内是否存在点Q,使得以O、P、D、Q为顶点四边形为菱形,若存在,请直接写出Q点坐标;若不存在,请说明理由.
【答案】(1)5,0;(2)t=5;(3)满足条件的点Q的坐标为:(8,4)、(﹣3,4)、(3,4)、(2.5,﹣4).
【解析】
(1)根据中点的定义求出OD的长即可解决问题;
(2)利用平行四边形的性质求出PC=5即可解决问题;
(3)分四种情形:当P1O=OD=5或P2O=P2D或P3D=OD=5或P4D=OD=5时,分别求解即可.
解:(1)∵A(10,0),OD=DA,
∴OA=10,OD=DA=5,
∴D(5,0).
故答案为5,0.
(2)∵四边形 PODB 是平行四边形,
∴PB=OD=5,
∴PC=5,
∴t=5.
(3)当P1O=OD=5时,由勾股定理可以求得P1C=3,可得Q1(8,4)
当P2O=P2D时,作P2E⊥OA,
∴OE=ED=2.5,可得Q2(2.5,﹣4),
当P3D=OD=5时,作DF⊥BC,由勾股定理,得P3F=3,
∴P3C=2,可得Q3(﹣3,4),
当P4D=OD=5时,作P4G⊥OA,由勾股定理,得DG=3,
∴OG=8,可得Q4(3,4),

综上所述,满足条件的点Q的坐标为:(8,4)、(﹣3,4)、(3,4)、(2.5,﹣4).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目