题目内容
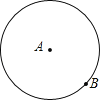
【题目】对于平面上两点A,B,给出如下定义:以点A或B为圆心,AB长为半径的圆称为点A,B的“确定圆”.如图为点A,B的“确定圆”的示意图.
(1)已知点A的坐标为(-1,0),点B的坐标为(3,3),则点A,B的“确定圆”的面积为______;
(2)已知点A的坐标为(0,0),若直线y=x+b上只存在一个点B,使得点A,B的“确定圆”的面积为9π,求点B的坐标;
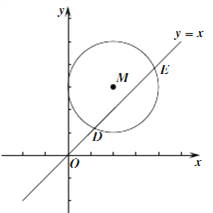
(3)已知点A在以P(m,0)为圆心,以1为半径的圆上,点B在直线![]() 上,若要使所有点A,B的“确定圆”的面积都不小于9π,直接写出m的取值范围.
上,若要使所有点A,B的“确定圆”的面积都不小于9π,直接写出m的取值范围.
【答案】(1)25π;(2)点B的坐标为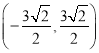 或
或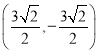 ;(3)m≤-5或m≥11
;(3)m≤-5或m≥11
【解析】
(1)根据勾股定理,可得AB的长,根据圆的面积公式,可得答案;
(2)根据确定圆,可得l与⊙A相切,根据圆的面积,可得AB的长为3,根据等腰直角三角形的性质,可得![]() ,可得答案;
,可得答案;
(3)根据圆心与直线垂直时圆心到直线的距离最短,根据确定圆的面积,可得PB的长,再根据30°的直角边等于斜边的一半,可得CA的长.
(1)(1)∵A的坐标为(1,0),B的坐标为(3,3),
∴AB=![]() =5,
=5,
根据题意得点A,B的“确定圆”半径为5,
∴S圆=π×52=25π.
故答案为25π;
(2)∵直线y=x+b上只存在一个点B,使得点A,B的“确定圆”的面积
为9π,
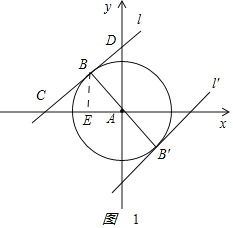
∴⊙A的半径AB=3且直线y=x+b与⊙A相切于点B,如图,
∴AB⊥CD,∠DCA=45°.
 ,
,
①当b>0时,则点B在第二象限.
过点B作BE⊥x轴于点E,
∵在Rt△BEA中,∠BAE=45°,AB=3,
∴![]() .
.
∴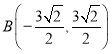 .
.
②当b<0时,则点B'在第四象限.
同理可得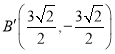 .
.
综上所述,点B的坐标为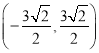 或
或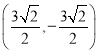 .
.
(3)如图2,
 ,
,
直线![]() 当y=0时,x=3,即C(3,0).
当y=0时,x=3,即C(3,0).
∵tan∠BCP=![]() ,
,
∴∠BCP=30°,
∴PC=2PB.
P到直线![]() 的距离最小是PB=4,
的距离最小是PB=4,
∴PC=8.
3-8=-5,P1(-5,0),
3+8=11,P(11,0),
当m≤-5或
点A,B的“确定圆”的面积都不小于9π,m的范围是m≤-5或m≥11.