题目内容
【题目】综合题
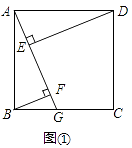
(1)如图①,四边形ABCD是正方形,点G是BC上的任意一点,BF⊥AG于点F,DE⊥AG于点E,探究BF,DE,EF之间的数量关系,第一学习小组合作探究后,得到DE﹣BF=EF,请证明这个结论; 
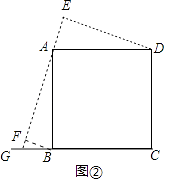
(2)若(1)中的点G在CB的延长线上,其余条件不变,请在图②中画出图形,并直接写出此时BF,DE,EF之间的数量关系; 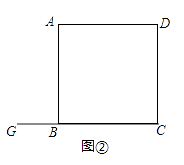
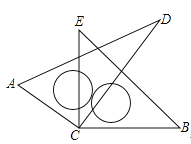
(3)如图③,四边形ABCD内接于⊙O,AB=AD,E,F是AC上的两点,且满足∠AED=∠BFA=∠BCD,试判断AC,DE,BF之间的数量关系,并说明理由 
【答案】
(1)解:如图1中,结论:DE﹣BF=EF.理由如下:
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵BF⊥AG于点F,DE⊥AG于点E,
∴∠AFB=∠DEA=90°,
∵∠BAF+∠DAE=90°,∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
在△ABF和△DAE中,
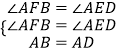 ,
,
∴△ABF≌△DAE,
∴BF=AE,AF=DE,
∵AF﹣AE=EF,
∴DE﹣BF=EF.
(2)解:结论EF=DE+BF.理由如下:
如图2中,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵BF⊥AG于点F,DE⊥AG于点E,
∴∠AFB=∠DEA=90°,
∵∠BAF+∠DAE=90°,∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
在△ABF和△DAE中,
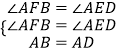 ,
,
∴△ABF≌△DAE,
∴BF=AE,AF=DE,
∴EF=AF+AF=DE+BF.
(3)解:如图3中,结论:AC=BF+DE.理由如下:
连接BD.

∵∠DBC+∠BDC+∠DCB=180°,∠DAE+∠ADE+∠AED=180°,
又∵∠DBC=∠DAE,∠DCB=∠AED,
∴∠ADE=∠BDC,
∵∠BDC=∠BAF,
∴∠ADE=∠BAF,∵AD=AB,∠AED=∠AFB,
∴△ADE≌△BAF,
∴AE=BF,
∵AD=AB,
∴∠ADB=∠ABD=∠ACD,
∵∠ADE=∠CDB,
∴∠CDE=∠ADB,
∴∠EDC=∠ECD,
∴DE=CE,
∴AC=BF+DE.
【解析】(1)如图1中,结论:DE﹣BF=EF.只要证明△ABF≌△DAE,即可解决问题.(2)结论EF=DE+BF.证明方法类似(1).(3)如图3中,结论:AC=BF+DE.只要证明△ADE≌△BAF以及DE=EC即可解决问题.

 导学全程练创优训练系列答案
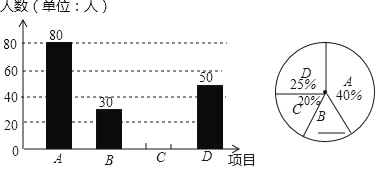
导学全程练创优训练系列答案【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )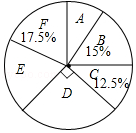
A.这次被调查的学生人数为200人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中最想选F的人数为35人
D.被调查的学生中最想选D的有55人
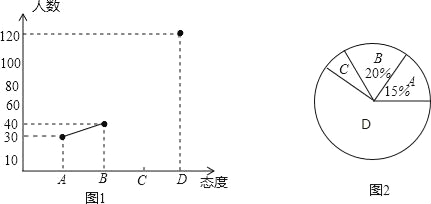
【题目】中学生带手机上学的现象越来越受到社会的关注,为此某记者随机调查了市区某校七年级若干名中学生家长对这种现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对).统计员在将测试数据绘制成图表时发现,反对漏统计6人,赞成漏统计4人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
家长对中学生带手机上学各项态度人数统计表和统计图:
态度 | 调整前人数 | 调整后人数 |
A.无所谓 | 30 | 30 |
B.基本赞成 | 40 | 40 |
C.赞成 | ||
D.反对 | 114 | 120 |
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)填写统计表,并根据调整后数据补全折线统计图;
(3)根据抽样调查结果,请你估计该市城区6000名中学生家长中有多少名家长持反对态度?