题目内容
【题目】以正方形![]() 的边
的边![]() 作等边三角形
作等边三角形![]() ,则
,则![]() 的度数是______________
的度数是______________![]() .
.
【答案】30°或150°
【解析】
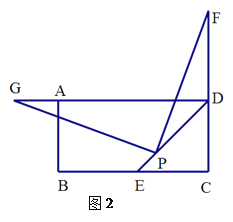
如果要求![]() 的度数,则要分两种情况讨论,第一种点
的度数,则要分两种情况讨论,第一种点![]() 在正方形
在正方形![]() 的内部,第二种情况点
的内部,第二种情况点![]() 在正方形
在正方形![]() 的外部,作图如下,利用正方形和等边三角形的性质及三角形内角和分别求出∠AEB和∠DEC的度数,图(1)是∠BEC=60°﹣(∠AEB+∠DEC),图(2)是∠BEC=360°﹣∠AEB﹣∠AED﹣∠DEC即可求解.
的外部,作图如下,利用正方形和等边三角形的性质及三角形内角和分别求出∠AEB和∠DEC的度数,图(1)是∠BEC=60°﹣(∠AEB+∠DEC),图(2)是∠BEC=360°﹣∠AEB﹣∠AED﹣∠DEC即可求解.
解:如图(1)中,当点E在正方形ABCD外时,
在正方形ABCD中,AB=BC=AD=CD,∠BAD=∠ADC=90°,AB∥CD,
在等边△ADE中,AD=DE=AE,∠ADE=∠AED=∠DAE=60°,
∴AB=AE=CD=DE;
∵AB=AE,
∴∠ABE=∠AEB=![]() (180°-∠BAE)=
(180°-∠BAE)=![]() (180°-90°-60°)=15°;
(180°-90°-60°)=15°;
同理可证∠DCE=∠DEC=15°,
∴在△AED中,
∠BEC=60°-(∠AEB+∠DEC)=60°﹣30°=30°.
∴∠BEC的度数是30°.
如图(2),当点E在正方形ABCD内时,
同理,∠BAD=∠ADC=90°,∠ADE=∠AED=∠DAE=60°,
∴∠BAE=∠CDE=30°;
∵AB=AE,
∴∠ABE=∠AEB=![]() (180°﹣30°)=75°;
(180°﹣30°)=75°;
同理∠DCE=∠DEC=![]() (180°﹣30°)=75°;
(180°﹣30°)=75°;
根据周角的定义,∠BEC=360°﹣∠BEA﹣∠AED﹣∠DEC=360°﹣75°﹣60°﹣75°=150°.
故答案是:30°或150°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目