Question

【题目】在正方形中，是边上一点（点不与点重合），连接．

（感知）如图1，过点作交于点．易证．（不需要证明）

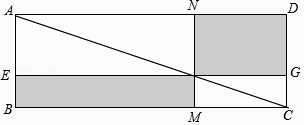
（探究）如图2，取的中点，过点作交于点，交于点．

（1）求证：．

（2）连接．若，则的长为___________．

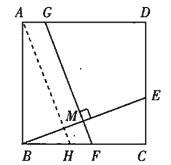
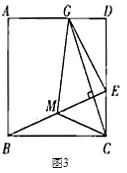
（应用）如图3，取的中点，连接．过点作交于点，连接．若，则四边形的面积为______．

Answer 1

【答案】【探究】（1）见解析；（2）2；【应用】9.

【解析】

（1）过A作，根据AD//BC，可证明四边形AHFG是平行四边形，可得AH=GF，由GF⊥BE可得AH⊥BE，利用直角三角形两锐角互余的性质可得∠BAH=∠CBE，利用ASA可证明△ABH≌△BCE，即可证明BE=AH，进而可得BE=FG；（2）连接CM，由（1）可知BE=FG，根据直角三角形斜边中线的性质可求出BE的长，即可得答案；【应用】根据直角三角形斜边中线的性质可得BE=6，ME=3，利用ASA可证明△BCE≌△CDG，可得BE=CG，利用三角形面积公式即可得答案.

（1）如图，过A作，

∵AD//BC，AH//GF，

∴四边形AHFG是平行四边形，

∴．

∵，

∴，

∴．

∵四边形是正方形，

∴，，

∴，

∴．

在和中，，，，

∴．

∴，

∴．

（2）连接CM，

∵∠BCD=90°，点M为BE中点，CM=1，

∴BE=2CM=2，

由（1）得BE=FG，

∴FG=2.

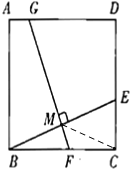
【应用】

在中，，是边上的中线，

∴．

∵∠DCG+∠BCG=90°，∠CBE+∠BCG=90°，

∴∠DCG+∠CBE，

又∵BC=CD，∠BCE=∠CDG=90°，

∴，

∴．

又∵，且，

∴．