题目内容
【题目】如图,AE∥BF,AC平分∠BAE,交BF于C. 
(1)尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);
(2)在(1)的图形中,找出两条相等的线段,并予以证明.
【答案】
(1)解:如图,BO为所作;
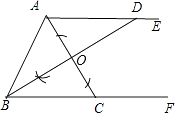
(2)解:AB=AD=BC.证明如下:
∵AE∥BF,
∴∠EAC=∠BCA,
∵AC平分∠BAE,
∴∠EAC=∠BAC,
∴∠BCA=∠BAC,
∴BA=BC,
∵BD⊥AO,AO平分∠BAD,
∴AB=AD,
∴AB=AD=BC
【解析】(1)利用基本作图作BO⊥AC即可;(2)先利用平行线的性质得∠EAC=∠BCA,再根据角平分线的定义和等量代换得到∠BCA=∠BAC,则BA=BC,然后根据等腰三角形的判定方法由BD⊥AO,AO平分∠BAD得到AB=AD,所以AB=AD=BC.

练习册系列答案
相关题目
【题目】某校八年级学生在学习《数据的分析》后,进行了检测,现将该校八(1)班学生的成绩统计如下表,并绘制成条形统计图(不完整). 
分数(分) | 人数(人) |
68 | 4 |
78 | 7 |
80 | 3 |
88 | 5 |
90 | 10 |
96 | 6 |
100 | 5 |
(1)补全条形统计图;
(2)该班学生成绩的平均数为86.85分,写出该班学生成绩的中位数和众数;
(3)该校八年级共有学生500名,估计有多少学生的成绩在96分以上(含96分)?
(4)小明的成绩为88分,他的成绩如何,为什么?