Question

【题目】如图，△ABC≌△ADE，BC的延长线交DA于F，交DE于G，∠ACB＝∠AED＝105°，∠CAD＝10°，∠B＝∠D＝25°，求∠DFB、∠DGB的度数．

Answer 1

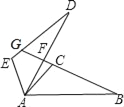
【答案】∠DFB＝85°；∠DGB＝60°．

【解析】

根据三角形的内角和定理求出∠BAC，再求出∠BAF，然后根据三角形的一个外角等于与它不相邻的两个内角的和分别求解即可．

∵∠ACB＝105°，∠B＝25°，

∴∠BAC＝180°﹣∠ACB﹣∠B＝180°﹣105°﹣25°＝50°，

∵∠CAD＝10°，

∴∠BAF＝∠BAC+∠CAD＝50°+10°＝60°，

在△ABF中，∠DFB＝∠B+∠BAF＝25°+60°＝85°；

∵∠D＝25°，

∴在△DGF中，∠DGB＝∠DFB﹣∠D＝85°﹣25°＝60°．