题目内容
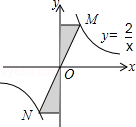
如图，A、B是反比例函数y=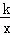
上两点，AC⊥y轴于C，BD⊥x轴于D，AC=BD=
OC，S四边形ABDC=14，则k= ____．
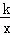上两点，AC⊥y轴于C，BD⊥x轴于D，AC=BD=OC，S四边形ABDC=14，则k= ____．16
试题分析：利用已知条件判断点A与点B的纵横坐标正好相反，从而设出点A的坐标，进而求得点B的坐标，利用SACDB=S△CED﹣S△AEB，求得点A的坐标后，用待定系数法确定出k的值．
解：如图，分别延长CA，DB交于点E，
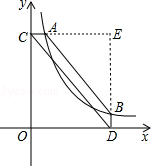
根据AC⊥y轴于C，BD⊥x轴于D，AC=BD=
OC，知△CED为直角三角形，且点A与点B的纵横坐标正好相反，
设点A的坐标为（xA，yA），则点B的坐标为（yA，xA），点E的坐标为（yA，yA），
四边形ACDB的面积为△CED的面积减去△AEB的面积．
CE=ED=yA，AE=BE=y﹣
yA，∴SACDB=S△CED﹣S△AEB=
[yA•yA﹣（yA﹣yA）（yA﹣yA）]=
yA2=14，∵yA＞0，∴yA=8，
点A的坐标为（2，8），
∴k=2×8=16．
故答案为：16．
点评：本题考查了反比例函数系数k的几何意义，关键是要构造直角三角形CED，利用SACDB=S△CED﹣S△AEB计算．
练习册系列答案
阅读快车系列答案
相关题目
，y1），B（2，y2）为反比例函数y=
图象上的两点，动点P（x，0）在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是（ ）
，0）
，0）
，0）
(x＞0)的图象
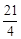D．2≤k≤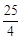
的图象有两个交点，当m= 时，有一个交点的纵坐标为6．
（x＞0）的图象上，顶点A1、B1分别在x轴、y轴的正半轴上，再在其右侧作正方形P2P3A2B2，顶点P3在反比例函数y=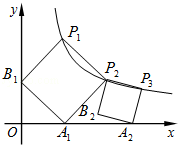
交于点A，B．过点A作AM⊥x轴，垂足为点M，连接BM．若S△ABM=1，则k的值是（ ）
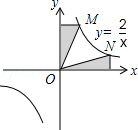
的图象大致是（ ）
（
为常数）的图象上有三点（－4，
），（－1，
），（2，
），则函数值