题目内容
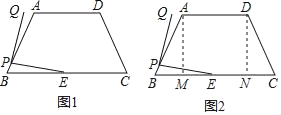
【题目】如图1,在四边形ABCD中,AD∥BC,AB=CD=13,AD=11,BC=21,E是BC的中点,P是AB上的任意一点,连接PE,将PE绕点P逆时针旋转90°得到PQ.
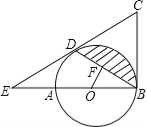
(1)如图2,过A点,D点作BC的垂线,垂足分别为M,N,求sinB的值;
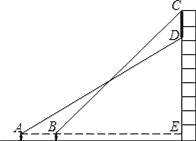
(2)若P是AB的中点,求点E所经过的路径弧EQ的长(结果保留π);
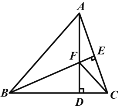
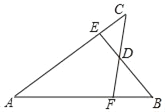
(3)若点Q落在AB或AD边所在直线上,请直接写出BP的长.
【答案】(1)![]() ;(2)5π;(3)PB的值为
;(2)5π;(3)PB的值为![]() 或
或![]() .
.
【解析】
(1)如图1中,作AM⊥CB用M,DN⊥BC于N,根据题意易证Rt△ABM≌Rt△DCN,再根据全等三角形的性质可得出对应边相等,根据勾股定理可求出AM的值,即可得出结论;
(2)连接AC,根据勾股定理求出AC的长,再根据弧长计算公式即可得出结论;
(3)当点Q落在直线AB上时,根据相似三角形的性质可得对应边成比例,即可求出PB的值;当点Q在DA的延长线上时,作PH⊥AD交DA的延长线于H,延长HP交BC于G,设PB=x,则AP=13﹣x,再根据全等三角形的性质可得对应边相等,即可求出PB的值.
解:(1)如图1中,作AM⊥CB用M,DN⊥BC于N.

∴∠DNM=∠AMN=90°,
∵AD∥BC,
∴∠DAM=∠AMN=∠DNM=90°,
∴四边形AMND是矩形,
∴AM=DN,
∵AB=CD=13,
∴Rt△ABM≌Rt△DCN,
∴BM=CN,
∵AD=11,BC=21,
∴BM=CN=5,
∴AM=![]() =12,
=12,
在Rt△ABM中,sinB=![]() =
=![]() .
.
(2)如图2中,连接AC.
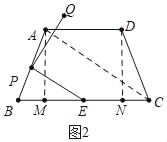
在Rt△ACM中,AC=![]() =
=![]() =20,
=20,
∵PB=PA,BE=EC,
∴PE=![]() AC=10,
AC=10,
∴![]() 的长=
的长=![]() =5π.
=5π.
(3)如图3中,当点Q落在直线AB上时,
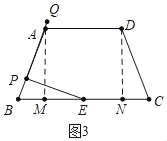
∵△EPB∽△AMB,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴PB=![]() .
.
如图4中,当点Q在DA的延长线上时,作PH⊥AD交DA的延长线于H,延长HP交BC于G.
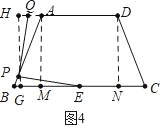
设PB=x,则AP=13﹣x.
∵AD∥BC,
∴∠B=∠HAP,
∴PG=![]() x,PH=
x,PH=![]() (13﹣x),
(13﹣x),
∴BG=![]() x,
x,
∵△PGE≌△QHP,
∴EG=PH,
∴![]() ﹣
﹣![]() x=
x=![]() (13﹣x),
(13﹣x),
∴BP=![]() .
.
综上所述,满足条件的PB的值为![]() 或
或![]() .
.

 教材全解字词句篇系列答案
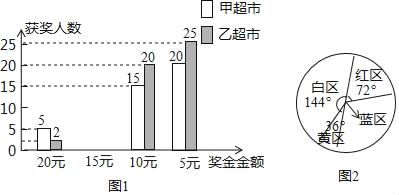
教材全解字词句篇系列答案【题目】两家超市同时采取通过摇奖返现金搞促销活动,凡在超市购物满100元的顾客均可以参加摇奖一次.小明和小华对两家超市摇奖的50名顾客获奖情况进行了统计并制成了图表(如图)
奖金金额 获奖人数 | 20元 | 15元 | 10元 | 5元 |
商家甲超市 | 5 | 10 | 15 | 20 |
乙超市 | 2 | 3 | 20 | 25 |
(1)在甲超市摇奖的顾客获得奖金金额的中位数是 ,在乙超市摇奖的顾客获得奖金金额的众数是 ;
(2)请你补全统计图1;
(3)请你分别求出在甲、乙两超市参加摇奖的50名顾客平均获奖多少元?
(4)图2是甲超市的摇奖转盘,黄区20元、红区15元、蓝区10元、白区5元,如果你购物消费了100元后,参加一次摇奖,那么你获得奖金10元的概率是多少?
【题目】某新建小区要修一条1050米长的路,甲、乙两个工程队想承建这项工程.经
了解得到以下信息(如表):
工程队 | 每天修路的长度(米) | 单独完成所需天数(天) | 每天所需费用(元) |
甲队 | 30 | n | 600 |
乙队 | m | n﹣14 | 1160 |
(1)甲队单独完成这项工程所需天数n= ,乙队每天修路的长度m= (米);
(2)甲队先修了x米之后,甲、乙两队一起修路,又用了y天完成这项工程(其中x,y为正整数).
①当x=90时,求出乙队修路的天数;
②求y与x之间的函数关系式(不用写出x的取值范围);
③若总费用不超过22800元,求甲队至少先修了多少米.