题目内容
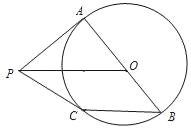
【题目】如图，AB是⊙O的直径，PA是⊙O的切线，点C在⊙O上，CB∥PO．
（1）判断PC与⊙O的位置关系，并说明理由；
（2）若AB=6，CB=4，求PC的长．
【答案】（1）PC是⊙O的切线，理由见解析；（2）
【解析】试题分析：（1）要证PC是⊙O的切线，只要连接OC，再证∠PCO=90°即可．
（2）可以连接AC，根据已知先证明△ACB∽△PCO，再根据勾股定理和相似三角形的性质求出PC的长．
试题解析：（1）结论：PC是⊙O的切线．
证明：连接OC
∵CB∥PO
∴∠POA=∠B，∠POC=∠OCB
∵OC=OB
∴∠OCB=∠B
∴∠POA=∠POC
又∵OA=OC，OP=OP
∴△APO≌△CPO
∴∠OAP=∠OCP
∵PA是⊙O的切线
∴∠OAP=90°
∴∠OCP=90°
∴PC是⊙O的切线．
（2）连接AC
∵AB是⊙O的直径
∴∠ACB=90°（6分）
由（1）知∠PCO=90°，∠B=∠OCB=∠POC
∵∠ACB=∠PCO
∴△ACB∽△PCO
∴
∴
．
练习册系列答案
相关题目
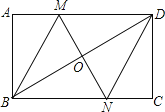
【题目】如图，在矩形ABCD中，对角线BD的垂直平分线MN与AD相交于点M，与BD相交于点O，与BC相交于点N，连接BM、DN．
求证：四边形BMDN是菱形；
若
，
，求菱形BMDN的面积和对角线MN的长．
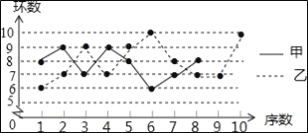
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹，成绩如表：
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且S乙2=1.8，根据上述信息完成下列问题：
（1）将甲运动员的折线统计图补充完整；
（2）乙运动员射击训练成绩的众数是_____，中位数是______．
（3）求甲运动员射击成绩的平均数和方差，并判断甲、乙两人本次射击成绩的稳定性．
