题目内容
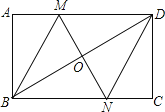
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于点N,连接BM、DN.
![]() 求证:四边形BMDN是菱形;
求证:四边形BMDN是菱形;
![]() 若
若![]() ,
,![]() ,求菱形BMDN的面积和对角线MN的长.
,求菱形BMDN的面积和对角线MN的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:
(1)先由已知条件证四边形BMDN是平行四边形,结合MN垂直平分BD即可得到平行四边形BMDN是菱形;
(2)设BM=x,由四边形BMDN是菱形可得DM=BM=x,由此可得AM=AD-DM=8-x,这样在Rt△ABM中由勾股定理可求得x=5,这样由S菱形BMDN=MD·AB即可求出其面积了;在Rt△ABD中由已知易得BD=![]() ,结合S菱形BMDN=MD·AB=
,结合S菱形BMDN=MD·AB=![]() BD·MN即可求得MN的长.
BD·MN即可求得MN的长.
(1)∵四边形ABCD是矩形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
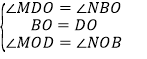 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形BMDN是平行四边形,
∵![]() ,
,
∴平行四边形BMDN是菱形.
(2)∵四边形BMDN是菱形,
∴![]() ,
,
设MD长为x,则![]() ,
,
在![]() 中,
中,![]()
即![]() ,
,
解得:![]() ,
,
即![]() .
.
菱形BMDN的面积![]() ,
,
∵![]() ,
,
又∵菱形BMDN的面积![]() ,
,
∴![]() .
.

练习册系列答案
相关题目