题目内容
【题目】快车从甲地驶向乙地,慢车从乙地驶向甲地,两车同时出发并且在同一条公路上匀速行驶,途中快车休息1.5小时,慢车没有休息.设慢车行驶的时间为x小时,快车行驶的路程为![]() 千米,慢车行驶的路程为
千米,慢车行驶的路程为![]() 千米.如图中折线OAEC表示
千米.如图中折线OAEC表示![]() 与x之间的函数关系,线段OD表示
与x之间的函数关系,线段OD表示![]() 与x之间的函数关系.
与x之间的函数关系.
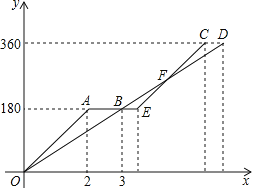
请解答下列问题:
(1)求快车和慢车的速度;
(2)求图中线段EC所表示的![]() 与x之间的函数表达式;
与x之间的函数表达式;
(3)线段OD与线段EC相交于点F,直接写出点F的坐标,并解释点F的实际意义.
【答案】(1)快车的速度为90千米/小时,慢车的速度为60千米/小时;(2)![]() ;(3)点F的坐标为
;(3)点F的坐标为![]() ,点F代表的实际意义是在4.5小时时,甲车与乙车行驶的路程相等.
,点F代表的实际意义是在4.5小时时,甲车与乙车行驶的路程相等.
【解析】
(1)根据函数图象中的数据可以求得快车和慢车的速度;
(2)根据函数图象中的数据可以求得点E和点C的坐标,从而可以求得![]() 与x之间的函数表达式;
与x之间的函数表达式;
(3)根据图象可知,点F表示的是快车与慢车行驶的路程相等,从而以求得点F的坐标,并写出点F的实际意义.
(1)快车的速度为:![]() 千米/小时,
千米/小时,
慢车的速度为:![]() 千米/小时,
千米/小时,
答:快车的速度为90千米/小时,慢车的速度为60千米/小时;
(2)由题意可得,
点E的横坐标为:![]() ,
,
则点E的坐标为![]() ,
,
快车从点E到点C用的时间为:![]() (小时),
(小时),
则点C的坐标为![]() ,
,
设线段EC所表示的![]() 与x之间的函数表达式是
与x之间的函数表达式是![]() ,
,
![]() ,得
,得![]() ,
,
即线段EC所表示的![]() 与x之间的函数表达式是
与x之间的函数表达式是![]() ;
;
(3)设点F的横坐标为a,
则![]() ,
,
解得,![]() ,
,
则![]() ,
,
即点F的坐标为![]() ,点F代表的实际意义是在4.5小时时,甲车与乙车行驶的路程相等.
,点F代表的实际意义是在4.5小时时,甲车与乙车行驶的路程相等.

【题目】每年5月份是心理健康宣传月,某中学开展以“关心他人,关爱自己”为主题的心理健康系列活动.为了解师生的心理健康状况,对全体2000名师生进行了心理测评,随机抽取20名师生的测评分数进行了以下数据的整理与
①数据收集:抽取的20名师生测评分数如下
85,82,94,72,78,89,96,98,84,65,73,54,83,76,70,85,83,63,92,90.
②数据整理:将收集的数据进行分组并评价等第:
分数x |
|
|
|
|
|
人数 | 5 | a | 5 | 2 | 1 |
等第 |
|
|
|
|
|
③数据绘制成不完整的扇形统计图:
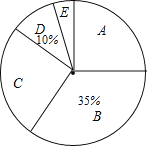
④依据统计信息回答问题
(1)统计表中的 .
(2)心理测评等第![]() 等的师生人数所占扇形的圆心角度数为 .
等的师生人数所占扇形的圆心角度数为 .
(3)学校决定对![]() 等的师生进行团队心理辅导,请你根据数据分析结果,估计有多少师生需要参加团队心理辅导?
等的师生进行团队心理辅导,请你根据数据分析结果,估计有多少师生需要参加团队心理辅导?
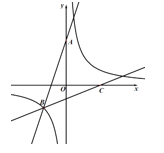
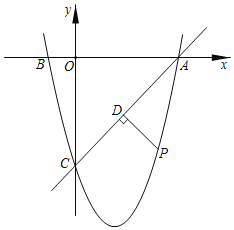
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() 、
、![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
![]() 求该函数的表达式;
求该函数的表达式;
![]() 点
点![]() 为该函数在第一象限内的图象上一点,过点
为该函数在第一象限内的图象上一点,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() .
.
①求线段![]() 的最大值;
的最大值;
②若以点![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.

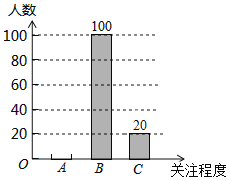
【题目】湖南省作为全国第三批启动高考综合改革的省市之一,从2018年秋季入学的高中一年级学生开始实施高考综合改革.深化高考综合改革,承载着广大考生的美好期盼,事关千家万户的切身利益,社会关注度高.为了了解我市某小区居民对此政策的关注程度,某数学兴趣小组随机采访了该小区部分居民,根据采访情况制做了如统计图表:
关注程度 | 频数 | 频率 |
A.高度关注 | m | 0.4 |
B.一般关注 | 100 | 0.5 |
C.没有关注 | 20 | n |
(1)根据上述统计图表,可得此次采访的人数为 ,m= ,n= .
(2)根据以上信息补全图中的条形统计图.
(3)请估计在该小区1500名居民中,高度关注新高考政策的约有多少人?