Question

【题目】阅读下面材料： 小明遇到这样两个问题：

（1）如图1，AB是⊙O的直径，C是⊙O上一点，OD⊥AC，垂足为D，BC=﹣6，求OD的长；
（2）如图2△ABC中，AB=6，AC=4，点D为BC的中点，求AD的取值范围． 对于问题（1），小明发现根据垂径定理，可以得出点D是AC的中点，利用三角形中位线定理可以解决；对于问题（2），小明发现延长AD到E，使DE=AD，连接BE，可以得到全等三角形，通过计算可以解决．

请回答：
问题（1）中OD长为；问题（2）中AD的取值范围是；
参考小明思考问题的方法，解决下面的问题：
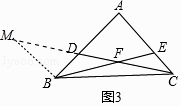
（3）如图3，△ABC中，∠BAC=90°，点D、E分别在AB、AC上，BE与CD相交于点F，AC=mEC，AB=2 EC，AD=nDB．
①当n=1时，如图4，在图中找出与CE相等的线段，并加以证明；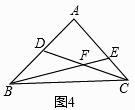

②直接写出 的值（用含m、n的代数式表示）．

Answer 1

【答案】
（1）解：如图1中，

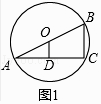
∵OD⊥AC，

∴AD=DC，

∵AO=OB，BC=6，

∴OD= BC=3．

（2）3；1＜AD＜5
（3）解：①结论：EF=CE．

理由：如图4中，延长CD到M使得DM=CD，连接BM．

∵AD=DB，∠ADC=∠BDM，

∴△ADC≌△BDM，

∴BM=AC，∠M=∠ACD，

∴BM∥AC，

∴△CEF∽△MBF，

∴ = ，

∴ = = ，

∴BF=mEF，

∴BE=（m+1）EF，

在Rt△BAE中，BE= = =（m+1）EC，

∴（m+1）EC=（m+1）EF，

∴EF=CE．

②结论： = ．

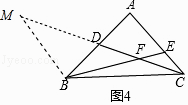
理由：如图3中，作BM∥AC交CD的延长线于M．

由△ADC∽△BDM，可得 = =n，

∴BM= ，

∵ = ，

∴ = ，

∵AC=mEC，

∴BF= EF，

∴BE=（1+ ）EF，

在Rt△BAE中，BE= = =（m+1）EC，

∴（m+1）EC=（1+ ）EF，

∴ = ．

【解析】（2）如图2中，延长AD到M，使得DM=AD，连接BM，CM．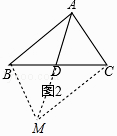
∵AD=DM，BD=CD，
∴四边形ABMC是平行四边形，
∴BM=AC=4，∵AB=6，
∴6﹣4＜AM＜6+4，
即2＜2AD＜10，
∴1＜AD＜5．