题目内容
【题目】如图,射线![]() 平分
平分![]() ,
,![]() 为射线
为射线![]() 上一点,以
上一点,以![]() 为圆心,10为半径作
为圆心,10为半径作![]() ,分别与
,分别与![]() 两边相交于
两边相交于![]() 、
、![]() 和
和![]() 、
、![]() ,连结
,连结![]() ,此时有
,此时有![]() .
.
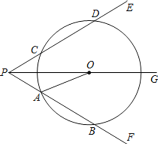
(1)求证:![]() ;
;
(2)若![]() ,求弦
,求弦![]() 的长;
的长;
【答案】(1)证明过程见解析;(2)12;
【解析】
(1)根据角平分线的定义可得∠DPO=∠BPO,然后根据平行线的性质可得∠DPO=∠POA,从而得出∠BPO=∠POA,然后根据等角对等边即可证出结论;
(2)过点O作OH⊥AB于点H,根据垂径定理可得![]() ,然后根据锐角三角函数证出PH=2OH,设OH=x,则PH=2x,根据勾股定理列出方程即可求出x,从而求出AH和AB.
,然后根据锐角三角函数证出PH=2OH,设OH=x,则PH=2x,根据勾股定理列出方程即可求出x,从而求出AH和AB.
(1)证明:∵PG平分∠EPF,
∴∠DPO=∠BPO,
∵OA∥PE,
∴∠DPO=∠POA,
∴∠BPO=∠POA,
∴PA=OA;
(2)解:过点O作OH⊥AB于点H,则![]()
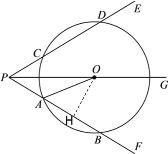
∵![]()
∴PH=2OH
设OH=x,则PH=2x,
由(1)可知PA=OA=10,
∴AH=PH-PA=2x-10,
∵AH2+OH2=OA2,
∴(2x-10)2+x2=102
解得x1=0(不合题意,舍去),x2=8,
∴AH=6,
∴AB=2AH=12;

练习册系列答案
相关题目