题目内容
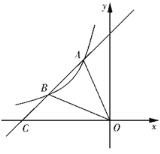
【题目】如图,在平面直角坐标中,抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3),点P是直线BC上方抛物线上的一动点,PE∥y轴,交直线BC于点E连接AP,交直线BC于点 D.
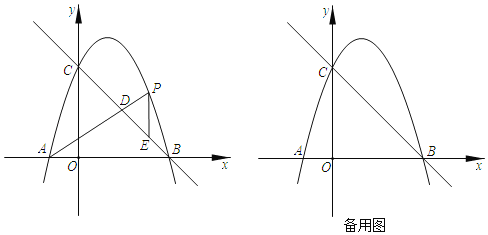
(1)求抛物线的函数表达式;
(2)当AD=2PD时,求点P的坐标;
(3)求线段![]() 的最大值;
的最大值;
(4)当线段![]() 最大时,若点F在直线BC上且∠EFP=2∠ACO,直接写出点F的坐标.
最大时,若点F在直线BC上且∠EFP=2∠ACO,直接写出点F的坐标.
【答案】(1)y=﹣x2+2x+3;(2)P(1,4)或P(2,3);(3)当t=2时,![]() 的值最大为4;(4)
的值最大为4;(4)![]()
【解析】
(1)由于抛物线与x轴的两个交点坐标已知,可把抛物线的解析式设成交点式,再代入另一已知点坐标便可求出解析式;
(2)过A作EF⊥x轴,与BC相交于点F,用待定系数法求出BC的解析式,设P点的横坐标为t,进而求得AF与PE,由相似三角形的比例线段求得t便可;
(3)根据PE关于t的函数解析式,由函数的性质求出其最大值便可;
(4)分两种情况:①当F点在PE的左边时,过点P作PM⊥BC于点M,过E作EN⊥x轴于点N,过点F作FQ⊥x轴于点Q,过点O作OG⊥AC于点G,取AC的中点H,连接OH,通过三角形相似求出MF的值便可;②将求得的F点坐标,关于PM对称点便是另一F点.
(1)设抛物线的解析式为:y=a(x+1)(x-3)(a≠0),
把C(0,3)代入得,3=a×1×(-3),
∴a=-1,
∴抛物线的解析式为:y=-(x+1)(x-3),即y=-x2+2x+3;
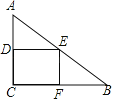
(2)过A作AF⊥x轴,与BC相交于点F,如图1,设P(t,﹣t2+2t+3),
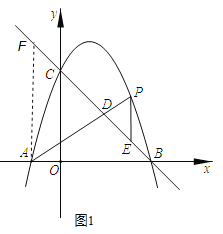
则AF∥PE,
设BC的解析式为y=kx+b(k≠0),则![]() ,
,
解得,![]() ,
,
∴直线BC的解析式为:y=﹣x+3,
∴E(t,﹣t+3),F(﹣1,4),
∴AF=4,PE=﹣t2+3t,
∵AF∥PE,
∴△AFD∽△PED,
∴![]() ,
,
∵AD=2PD,
∴![]() ,解得,t=1或2,
,解得,t=1或2,
∴P(1,4)或P(2,3);
(3)∵PE的解析式为:PE=﹣t2+3t
过点E作EH⊥y轴,如图2
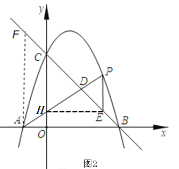
∴![]()
∴![]()
∴当t=2时,![]() 的值最大为4;
的值最大为4;
(4)①当F点在
过点P作PM⊥BC于点M,过E作EN⊥x轴于点N,过点F作FQ⊥x轴于点Q,过点O作OG⊥AC于点G,取AC的中点H,连接OH,如图3,

由(3)知,当![]() 取最大值时,P(2,3),PE=2,E(2,1),
取最大值时,P(2,3),PE=2,E(2,1),
∵OB=OC=3,
∴∠OBC=∠OCB=45°,
∴BE=![]() ,∠PEM=45°,
,∠PEM=45°,
∴PM=EM=![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,∠OHG=2∠ACO,
,∠OHG=2∠ACO,
∵∠EFP=2∠ACO,
∴∠EFP=∠OHG,
∵∠OGH=∠PMF,
∴△OGH∽△PMF,
∴![]() ,即
,即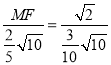 ,
,
∴MF=![]() ,
,
∴BF=BE+EM+MF=![]() ,
,
∴FQ=BQ=![]() ,
,
∴OQ=BQ-BO=![]() ,
,
∴F(![]() ,
,![]() ),
),
②当F点在PE的右边时,此时的F点恰好与(![]() ,
,![]() )关于PM对称,易求此时F(
)关于PM对称,易求此时F(![]() ,
,![]() ).
).
故F的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).