题目内容
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,下列四个结论:
,下列四个结论:
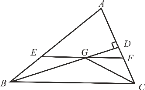
①![]() ; ②
; ②![]() ;
;
③点![]() 到
到![]() 各边的距离相等;
各边的距离相等;
④设![]() ,
,![]() ,则
,则![]() .
.
其中正确的结论有( )
A.①②④B.①②③C.①③④D.①②③④
【答案】B
【解析】
由在△ABC中,∠ABC和∠ACB的平分线相交于点G,根据角平分线的定义与三角形内角和定理,即可求得②∠BGC=90°+![]() ∠A正确;由平行线的性质和角平分线的定义得出△BEG和△CFG是等腰三角形得出EF=BE+CF故①正确;由角平分线的性质得出点G到△ABC各边的距离相等,故③正确;由角平分线定理与三角形面积的求解方法,即可求得③设GD=m,AE+AF=n,则S△AEF=
∠A正确;由平行线的性质和角平分线的定义得出△BEG和△CFG是等腰三角形得出EF=BE+CF故①正确;由角平分线的性质得出点G到△ABC各边的距离相等,故③正确;由角平分线定理与三角形面积的求解方法,即可求得③设GD=m,AE+AF=n,则S△AEF=![]() mn,故④错误.
mn,故④错误.
解:∵在△ABC中,∠ABC和∠ACB的平分线相交于点G,
∴∠GBC=![]() ∠ABC,∠GCB=
∠ABC,∠GCB=![]() ∠ACB,∠A+∠ABC+∠ACB=180°,
∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠GBC+∠GCB=90°-![]() ∠A,
∠A,
∴∠BGC=180°-(∠GBC+∠GCB)=90°+![]() ∠A;故②正确;
∠A;故②正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点G,
∴∠GBC=∠GBE,∠GCB=∠GCF,
∵EF∥BC,
∴∠GBC=∠EGB,∠GCB=∠FGC,
∴∠EGB=∠GBE,∠FGC=∠GCF,
∴BE=GE,CF=GF,
∴EF=GE+GF=BE+CF,
故①正确;
过点G作GM⊥AB于M,作GN⊥BC于N,连接GA,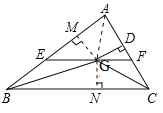
∵在△ABC中,∠ABC和∠ACB的平分线相交于点G,
∴GN=GD=GM=m,
∴S△AEF=S△AGE+S△AGF=![]() AEGM+
AEGM+![]() AFGD=
AFGD=![]() GD(AE+AF)=
GD(AE+AF)=![]() mn;故④错误;
mn;故④错误;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点G,
∴点G到△ABC各边的距离相等,故③正确.
故选:B.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共![]() 个,某学习小组做摸球试验,将球搅匀后,从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
个,某学习小组做摸球试验,将球搅匀后,从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
![]() 请估计:当
请估计:当![]() 很大时,摸到白球的频率将会接近于多少?
很大时,摸到白球的频率将会接近于多少?
摸球的次数 |
|
|
|
|
|
|
摸到白球的次数 |
|
|
|
|
|
|
摸到白球的概率 |
|
|
|
|
|
|
![]() 假如你去摸一次,你摸到白球的可能性为多大?这时摸到黑球的可能性为多大?
假如你去摸一次,你摸到白球的可能性为多大?这时摸到黑球的可能性为多大?
![]() 试估算口袋中黑、白两种颜色的球各有多少个?
试估算口袋中黑、白两种颜色的球各有多少个?