题目内容
【题目】如图所示，在平面直角坐标系中，抛物线y=ax2+bx+3经过A（﹣3，0），B（1，0）两点，与y轴交于点C，其顶点为D，连接AD，点P是线段AD上一个动点（不与A，D重合），过点P作y轴的垂线，垂足点为E，连接AE．
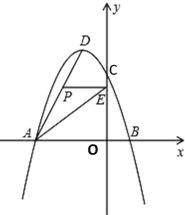
（1）求抛物线的函数解析式，并写出顶点D的坐标；
（2）如果P点的坐标为（x，y），△PAE的面积为S，求S与x之间的函数关系式，直接写出自变量x的取值范围，并求出S的最大值．
【答案】（1）y=﹣（x+1）2+4，D（﹣1，4）；（2）当x=
时，S取最大值
【解析】
（1）将点A和点B的坐标代入抛物线的解析式得到关于a、b的方程组，然后求得a、b的值可得到抛物线的解析式，然后利用配方法可求得抛物线的解析式；
（2）先求得直线AD的解析式，然后可得到P（x，2x+6）．接下来依据S=
PEyP可得到S与x的函数关系式，然后利用二次函数的性质可求得S的最大值以及此时x的值．
（1）∵抛物线y=ax2+bx+3经过A（﹣3，0）、B（1，0）两点
∴
，
解得
，
∴解析式为y=﹣x2﹣2x+3
∵y=﹣x2﹣2x+3=﹣（x+1）2+4，
∴抛物线顶点坐标D为（﹣1，4）．
（2）设AD为解析式为y=kx+b，且过点A（﹣3，0），D（﹣1，4），
则有
，解得
∴AD的解析式为：y=2x+6，
∵P在AD上，
∴P（x，2x+6），
∴S =PEyP=（﹣x）（2x+6）
=﹣x2﹣3x（﹣3＜x＜﹣1），
当x=
时，S取最大值．
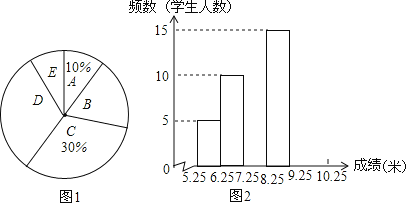
【题目】为了了解同学们每月零花钱的数额，校园小记者随机调查了本校部分同学，根据调查结果，绘制了如下尚不完整的统计图表：
组别 | A | B | C | D | E |
分组（元） | 0≤x<30 | 30≤x<60 | 60≤x<90 | 90≤x<120 | 120≤x<150 |
频数 | 4 | a | 20 | 8 | 2 |
请根据以上图标，解答下列问题：
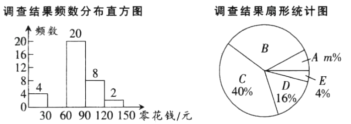
（1）填空：这次调查的样本容量是 ，a= ，m= ；
（2）补全频数分布直方图；
（3）求扇形统计图中扇形B的圆心角度数；
（4）该校共有1000人，请估计每月零花钱的数额x在30≤x<90范围的人数；
