题目内容
23、如图所示，已知等腰梯形ABCD中，AD∥BC，AB=CD，点E为梯形外一点，且AE=DE．求证：BE=CE．
分析：首先求出∠EAB=∠EDC．根据全等三角形的判定推出△ABE≌△DCE即可求解．
解答：证明：在等腰梯形ABCD中，AB=CD，
∴∠BAD=∠CDA，
∵EA=ED，
∴∠EAD=∠EDA，
∴∠EAB=∠EDC．
在△ABE和△DCE中，
∵AB=DC，∠EAB=∠EDC，EA=ED，
∴△ABE≌△DCE，
∴EB=EC．
∴∠BAD=∠CDA，
∵EA=ED，
∴∠EAD=∠EDA，
∴∠EAB=∠EDC．
在△ABE和△DCE中，
∵AB=DC，∠EAB=∠EDC，EA=ED，
∴△ABE≌△DCE，
∴EB=EC．
点评：本题考查全等三角形的判定定理以及等腰梯形的性质．
练习册系列答案
相关题目
10、如图所示，已知等腰梯形ABCD的中位线EF的长为6，腰AD的长为5，则该等腰梯形的周长为（ ）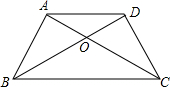
如图所示，已知等腰梯形ABCD中，AD∥BC，AB=DC，AC与BD相交于点O．请在图中找出一对全等的三角形，并加以证明．
如图所示，已知等腰梯形ABCD中，AD∥BC，AB=CD，∠A=105°，则∠C等于（ ）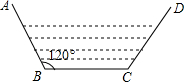
某村计划修建一条水渠，其横断面是等腰梯形，底角B为120°，如图所示，已知等腰梯形ABCD两腰与底边BC的和为4m，则梯形的最大面积为