题目内容
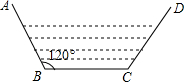 某村计划修建一条水渠,其横断面是等腰梯形,底角B为120°,如图所示,已知等腰梯形ABCD两腰与底边BC的和为4m,则梯形的最大面积为
某村计划修建一条水渠,其横断面是等腰梯形,底角B为120°,如图所示,已知等腰梯形ABCD两腰与底边BC的和为4m,则梯形的最大面积为分析:过B作AD的垂线BE于点E,设AB=xm,利用x表示出高BE和AD、BC的长,利用x表示梯形的面积,然后利用函数的性质即可求解.
解答: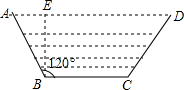 解:过B作AD的垂线BE于点E.
解:过B作AD的垂线BE于点E.
则∠ABE=120°-90°=30°.
设AB=xm,则BC=4-2xm,
在直角△ABE中,BE=AB•cos∠ABE=
xm,AE=
AB=
xm,
则AD=x+BC=x+(4-2x)=4-xm,
则梯形ABCD的面积y=
(AD+BC)•BE=
(4-x+4-2x)•
x,
即y=-
x2+2x,
则当x=
=
=
时,最大值是:-
×(
)2+2×
=
(m2).
故答案是:
.
 解:过B作AD的垂线BE于点E.
解:过B作AD的垂线BE于点E.则∠ABE=120°-90°=30°.
设AB=xm,则BC=4-2xm,
在直角△ABE中,BE=AB•cos∠ABE=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则AD=x+BC=x+(4-2x)=4-xm,
则梯形ABCD的面积y=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
即y=-
3
| ||
| 4 |
则当x=
| 2 | ||||
|
| 4 | ||
3
|
4
| ||
| 9 |
3
| ||
| 4 |
4
| ||
| 9 |
4
| ||
| 9 |
4
| ||
| 9 |
故答案是:
4
| ||
| 9 |
点评:本题考查等腰梯形的计算和二次函数等知识,考查求函数的解析式和求函数的最值问题,求最值的问题常用的方法是转化为函数的问题求解.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目