��Ŀ����
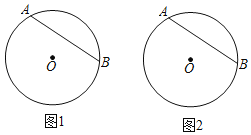
����Ŀ����ͼ���ڵȱ�![]() �У�
��![]() ������
������![]() �ӵ�
�ӵ�![]() ������
������![]() ���ٶ���
���ٶ���![]() �����˶�������
�����˶�������![]() ͬʱ�ӵ�
ͬʱ�ӵ�![]() ������ͬ�����ٶ���
������ͬ�����ٶ���![]() ���ӳ��߷��������˶�������
���ӳ��߷��������˶�������![]() �����
�����![]() ʱ����
ʱ����![]() ͬʱֹͣ�˶������˶�ʱ��Ϊ��
ͬʱֹͣ�˶������˶�ʱ��Ϊ��![]() ������
������![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ����
����![]() ����
����![]() Ϊ����ƽ���ı���
Ϊ����ƽ���ı���![]() ��
��
��1����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
��2���Ƿ����ijһʱ��![]() ��ʹ��
��ʹ��![]() ��
��![]() ��ƽ�����ϣ������ڣ����
��ƽ�����ϣ������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
��3����![]() �ij���
�ij���
��4��ȡ�߶�![]() ���е�
���е�![]() ������
������![]() ����
����![]() ��ֱ��
��ֱ��![]() ���ۣ���
���ۣ���![]() ������
������![]() ����
����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��ֵ��С���������Сֵ��
��ֵ��С���������Сֵ��

���𰸡���1��![]() ʱ��
ʱ��![]() ��ֱ�������Σ���2��
��ֱ�������Σ���2��![]() �����ڣ�����������3��3����4��
�����ڣ�����������3��3����4��![]() ����СֵΪ
����СֵΪ![]() ��
��
��������
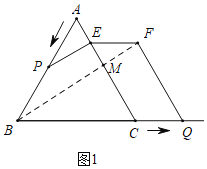
��1����![]() ʱ��
ʱ��![]() ���ɴ˹������̼��ɽ�����⣮
���ɴ˹������̼��ɽ�����⣮
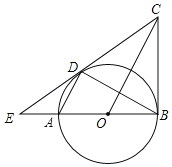
��2����ͼ1�У�����BF��![]() ��
��![]() ��֤��
��֤��![]() ���ɴ˹������̼��ɽ�����⣮
���ɴ˹������̼��ɽ�����⣮
��3��֤��![]() ���ɽ�����⣮
���ɽ�����⣮
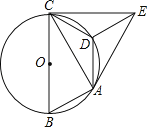
��4����ͼ3�У�����![]() ������
������![]() ��⼴�ɽ�����⣮
��⼴�ɽ�����⣮
�⣺��1����![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]() ��
��
�൱![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ʱ��
ʱ��![]() ��ֱ�������Σ�
��ֱ�������Σ�
��2�����ڣ�
���ɣ���ͼ1�У�����![]() ��
��![]() ��
��![]() ��
��
��![]() ƽ��
ƽ��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
���![]() ��
��
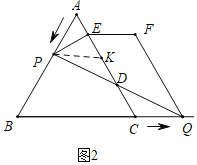
��3����ͼ2�У���![]() ��
��![]() ��
��![]() ��
��
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��4����ͼ3�У�����![]()

��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ����СֵΪ
����СֵΪ![]() ��
��

����Ŀ��ij�̵�����һ����Ʒ��ͯ�����г����鷢�֣�����Ʒ����������![]() ���������ۼ�
���������ۼ�![]() ��Ԫ/������һ�κ��������ۼۡ���������������������
��Ԫ/������һ�κ��������ۼۡ���������������������![]() ��Ԫ���������Ӧֵ���±���
��Ԫ���������Ӧֵ���±���
�ۼ� | 50 | 60 | 80 |
�������� | 100 | 80 | 40 |
���������� | 1000 | 1600 | 1600 |
ע�������������������������ۼۣ����ۣ�
��1������![]() ����
����![]() �ĺ�������ʽ����Ҫ��д���Ա�����ȡֵ��Χ��
�ĺ�������ʽ����Ҫ��д���Ա�����ȡֵ��Χ��
�ڸ���Ʒ������_________Ԫ/�������ۼ���________Ԫ/��ʱ������������������������__________Ԫ
��2������ij��ԭ����Ʒ���������![]() Ԫ/��
Ԫ/��![]() ����۲��Ź涨����Ʒ�ۼ۲��ó���65Ԫ/�������̵��ڽ��������У������������ۼ���Ȼ���㣨1���еĺ�����ϵ�������������������1400Ԫ����
����۲��Ź涨����Ʒ�ۼ۲��ó���65Ԫ/�������̵��ڽ��������У������������ۼ���Ȼ���㣨1���еĺ�����ϵ�������������������1400Ԫ����![]() ��ֵ
��ֵ