题目内容
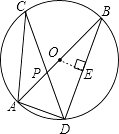
【题目】如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=40°,∠APD=65°. 
(1)求∠B的大小;
(2)已知圆心0到BD的距离为3,求AD的长.
【答案】
(1)解:∵∠CAB=∠CDB(同弧所对的圆周角相等),∠CAB=40°,
∴∠CDB=40°;
又∵∠APD=65°,
∴∠BPD=115°;
∴在△BPD中,
∴∠B=180°﹣∠CDB﹣∠BPD=25°
(2)解:过点O作OE⊥BD于点E,则OE=3.
∵AB是直径,
∴AD⊥BD(直径所对的圆周角是直角);
∴OE∥AD;
又∵O是AB的中点,
∴OE是△ABD的中位线,
∴AD=2OE=6.
【解析】(1)由同弧所对的圆周角相等求得∠CAB=∠CDB=40°,然后根据平角是180°求得∠BPD=115°;最后在△BPD中依据三角形内角和定理求∠B即可;(2)过点O作OE⊥BD于点E,则OE=3.根据直径所对的圆周角是直角,以及平行线的判定知OE∥AD;又由O是直径AB的半径可以判定O是AB的中点,由此可以判定OE是△ABD的中位线;最后根据三角形的中位线定理计算AD的长度.
【考点精析】关于本题考查的三角形的内角和外角和三角形中位线定理,需要了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能得出正确答案.

练习册系列答案
相关题目








