Question

【题目】在平面直角坐标系中，边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上，点O在原点．现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y=x上时停止旋转，旋转过程中，AB边交直线y=x于点M ， BC边交x轴于点N（如图）．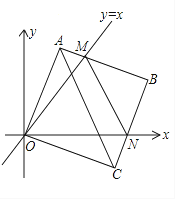

（1）求边OA在旋转过程中所扫过的面积；
（2）旋转过程中，当MN和AC平行时，求正方形OABC旋转的度数；
（3）设△MBN的周长为p ， 在旋转正方形OABC的过程中，p值是否有变化？请证明你的结论．

Answer 1

【答案】
（1）

解：∵A点第一次落在直线y=x上时停止旋转，直线y=x与y轴的夹角是45°，

∴OA旋转了45°．

∴OA在旋转过程中所扫过的面积为

（2）

解：∵MN∥AC，

∴∠BMN=∠BAC=45°，∠BNM=∠BCA=45°．

∴∠BMN=∠BNM．∴BM=BN．

又∵BA=BC，∴AM=CN．

又∵OA=OC，∠OAM=∠OCN，∴△OAM≌△OCN．

∴∠AOM=∠CON= （∠AOC-∠MON）= （90°-45°）=22.5°．

∴旋转过程中，当MN和AC平行时，正方形OABC旋转的度数为45°-22.5°=22.5°．

（3）

解：在旋转正方形OABC的过程中，p值无变化．

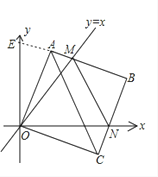
证明：延长BA交y轴于E点，

则∠AOE=45°-∠AOM，∠CON=90°-45°-∠AOM=45°-∠AOM，

∴∠AOE=∠CON．

又∵OA=OC，∠OAE=180°-90°=90°=∠OCN．

∴△OAE≌△OCN．

∴OE=ON，AE=CN．

又∵∠MOE=∠MON=45°，OM=OM，

∴△OME≌△OMN．∴MN=ME=AM+AE．

∴MN=AM+CN，

∴p=MN+BN+BM=AM+CN+BN+BM=AB+BC=4．

∴在旋转正方形OABC的过程中，p值无变化．

【解析】（1）根据扇形的面积公式来求得边OA在旋转过程中所扫过的面积；（2）解决本题需利用全等，根据正方形一个内角的度数求出∠AOM的度数；（3）利用全等把△MBN的各边整理到成与正方形的边长有关的式子．