题目内容
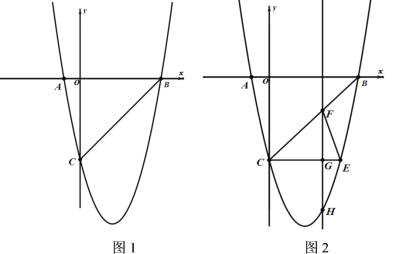
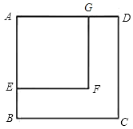
【题目】(1)如图,正方形![]() 的边
的边![]() ,
,![]() 分别在正方形
分别在正方形![]() 的边
的边![]() ,
,![]() 上.
上.
填空:![]() 和
和![]() 的数量关系是
的数量关系是 ![]() 和
和![]() 的位置关系是 .
的位置关系是 .
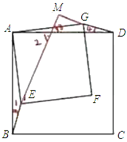
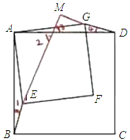
(2)把正方形![]() 绕点
绕点![]() 旋转到如图位置,(1)中的结论是否成立?若成立,写成证明过程,若不存在,请说明理由.
旋转到如图位置,(1)中的结论是否成立?若成立,写成证明过程,若不存在,请说明理由.
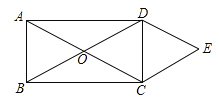
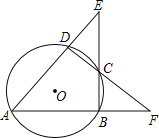
(3)设正方形![]() 的边长为4,正方形
的边长为4,正方形![]() 的边长为
的边长为![]() ,正方形
,正方形![]() 绕点
绕点![]() 旋转过程中,若
旋转过程中,若![]() 、
、![]() 、
、![]() 三点共线,求
三点共线,求![]() 的长.(直接写出结果)
的长.(直接写出结果)
【答案】(1) ![]() ;
; ![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() 或
或![]()
【解析】
(1)根据正方形的性质即可求解;
(2)先证明![]() ,得到
,得到![]() ,由
,由![]() 得到
得到![]() ,再利用
,再利用![]() 得到
得到![]() ,即可得到
,即可得到![]() ;
;
(3)根据分两种情况讨论作图①连接![]() 交
交![]() 于
于![]() ,②连接
,②连接![]() 交
交![]() 于
于![]() ,根据含30°的直角三角形的性质即可求解.
,根据含30°的直角三角形的性质即可求解.
(1)∵正方形![]() 的边
的边![]() ,
,![]() 分别在正方形
分别在正方形![]() 的边
的边![]() ,
,![]() 上
上
∴AG=AE,AD=AB,AB⊥AD
∴AD-AG=AB-AE,
即![]() ,
,![]()
故填:![]() ;
; ![]() ;
;
(2)证明:由题知:
![]()
![]()
![]()
![]()
![]()
在![]() 和
和![]() 中
中
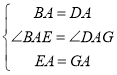
![]()
![]()
![]()
![]()
又![]()
![]()
![]()
即![]()
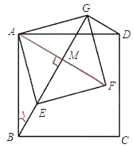
(3)答:![]() 或
或![]()
①连接![]() 交
交![]() 于
于![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
②连接![]() 交
交![]() 于
于![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目