题目内容
【题目】如图6,在平面直角坐标系中,一次函数![]() =
=![]() +1的图象交
+1的图象交![]() 轴于点D,与反比例函数
轴于点D,与反比例函数![]() =
=![]() 的图象在第一象限相交于点A.过点A分别作
的图象在第一象限相交于点A.过点A分别作![]() 轴
轴![]() 轴的垂线,垂足为点BC.
轴的垂线,垂足为点BC.
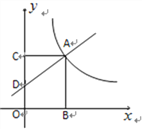
(1)点D的坐标为 ;
(2)当AB=4AC时,求![]() 值;
值;
(3)当四边形OBAC是正方形时,直接写出四边形ABOD与△ACD面积的比.
【答案】(1) D(0,1); (2)![]() ;(3)5:3.
;(3)5:3.
【解析】分析:
(1)在y=kx+1中,由x=0可得y=1,由此可得点D的坐标为(0,1);
(2)设点A的坐标为(a,b),由题意可得b=4a,代入反比例函数的解析式![]() 即可解得a的值,从而得到点A的坐标,把所得坐标代入y=kx+1中即可求得k的值;
即可解得a的值,从而得到点A的坐标,把所得坐标代入y=kx+1中即可求得k的值;
(3)由题意可设点A的坐标为(m,m),代入![]() 中,求得m的值,即可得到此时点A的坐标,结合点D的坐标即可求得四边形ABOD和△ACD的面积,从而可求得两个图形的面积比.
中,求得m的值,即可得到此时点A的坐标,结合点D的坐标即可求得四边形ABOD和△ACD的面积,从而可求得两个图形的面积比.
详解:
(1)∵在y=kx+1中,当x=0时,y=1,
∴点D的坐标为:(0,1);
(2)设点A(a,b),
∵点A在第一象限,
∴a与b均大于0,即AB=b,AC=a,
∵AB=4AC,
∴得b=4a,
代入反比例函数解析式![]() ,得
,得![]() ,
,
解得:a=2或a=-2(不合题意,舍去),
∴A的坐标为A(2,8),
代入一次函数y=kx+1得:8=2k+1,
解得:![]() ;
;
(3)∵四边形OBAC是正方形,
∴OB=AB,
∴可设点A的坐标为(m,m),
代入![]() 得:
得:![]() ,解得m=4或m=-4(不合题意,舍去),
,解得m=4或m=-4(不合题意,舍去),
∴点A的坐标为(4,4),
∴AB=OB=AC=OC=4,
又∵点D的坐标为(0,1),
∴OD=1,CD=3,
∴S△ACD=![]() AC·CD=6,S四边形OBAD=
AC·CD=6,S四边形OBAD=![]() (AB+OD)·OB=10,
(AB+OD)·OB=10,
∴S四边形OBAD:S△ACD=5:3.

【题目】前不久在台湾抗震救灾中,某地将甲、乙两个仓库的粮食全部转移到A、B两个仓库.甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A,B两库的路程和运费如下表:
路程(km) | 运费(元/吨km) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)函数关系式.
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?