题目内容
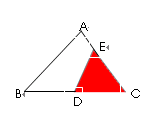
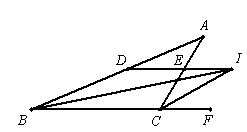
如图,四边形ABCD中,∠BAD=∠C=90º,AB=AD,AE⊥BC于E,若线段AE=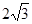 ,则S四边形ABCD= 。
,则S四边形ABCD= 。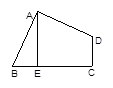
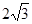 ,则S四边形ABCD= 。
,则S四边形ABCD= 。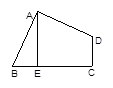
12
试题分析:
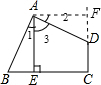
过A点作AF⊥CD交CD的延长线于F点,如图,
∵AE⊥BC,AF⊥CF,
∴∠AEC=∠CFA=90°,
而∠C=90°,
∴四边形AECF为矩形,
∴∠2+∠3=90°,
又∵∠BAD=90°,
∴∠1=∠2,
在△ABE和△ADF中:
∠1=∠2,∠AEB=∠AFD,AB=AD
∴△ABE≌△ADF,
∴AE=AF=
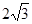 ,S△ABE=S△ADF,
,S△ABE=S△ADF,∴四边形AECF是边长为5的正方形,
∴S四边形ABCD=S正方形AECF=(
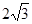 )2=12.
)2=12.故答案为12.
点评:本题考查了全等三角形的判定与性质:有两组对应角相等,并且有一条边对应相等的两个三角形全等;全等三角形的对应边相等;全等三角形的面积相等.也考查了矩形的性质.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
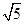 的格点直角三角形;
的格点直角三角形;
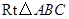 中,
中,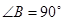 ,
,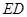 是
是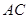 的垂直平分线,交
的垂直平分线,交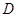 ,交
,交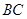 于点
于点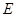 .已知
.已知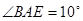 ,则
,则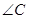 的度数为 ____________
的度数为 ____________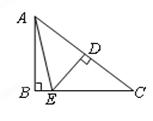
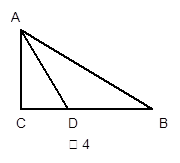
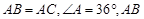 的中垂线
的中垂线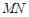 交
交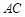 于点
于点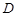 ,交
,交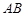 于点
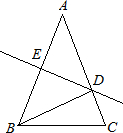
于点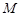 ,有下面4个结论:①射线
,有下面4个结论:①射线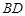 是
是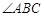 的角平分线;②图中共有三个等腰三角形;③
的角平分线;②图中共有三个等腰三角形;③ 的周长=AB+BC;④
的周长=AB+BC;④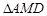 ≌
≌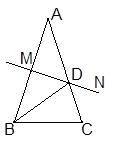
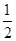 EC, 则
EC, 则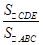 = 。
= 。