题目内容
已知a，b，c是三角形的三边，那么代数式a2-2ab+b2-c2的值
- A.大于零
- B.等于零
- C.小于零
- D.不能确定
C
分析：根据三角形中任意两边之和大于第三边．把代数式a2-2ab+b2-c2分解因式就可以进行判断．
解答：a2-2ab+b2-c2=（a-b）2-c2=（a+c-b）[a-（b+c）]．
∵a，b，c是三角形的三边．
∴a+c-b＞0，a-（b+c）＜0．
∴a2-2ab+b2-c2＜0．
故选C．
点评：本题考查了三角形中三边之间的关系．（a+c-b）[a-（b+c）]是一个正数与负数的积，所以小于0．
分析：根据三角形中任意两边之和大于第三边．把代数式a2-2ab+b2-c2分解因式就可以进行判断．
解答：a2-2ab+b2-c2=（a-b）2-c2=（a+c-b）[a-（b+c）]．
∵a，b，c是三角形的三边．
∴a+c-b＞0，a-（b+c）＜0．
∴a2-2ab+b2-c2＜0．
故选C．
点评：本题考查了三角形中三边之间的关系．（a+c-b）[a-（b+c）]是一个正数与负数的积，所以小于0．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
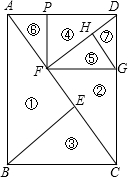知线段AB=1，∠BAC=θ．
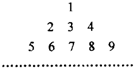（2011•崇川区模拟）已知正整数1，2，3，4，5，6，7，8，9，…按如下方式排列成三角形状，则第10行第12个数是（ ）