题目内容
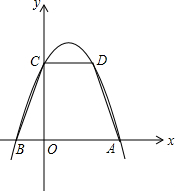 如图,在直角坐标系中,等腰梯形ABCD中,AB∥CD,AD=BC=
如图,在直角坐标系中,等腰梯形ABCD中,AB∥CD,AD=BC= ,AB=4,CD=2.抛物线y=ax2+bx+c经过A、B、C三点.
,AB=4,CD=2.抛物线y=ax2+bx+c经过A、B、C三点.
(1)求抛物线的函数表达式;
(2)点E是x轴上一点,且以E、A、D、C为顶点的四边形是平行四边形.若过B点的直线把这个四边形的面积分成相等的两部分,求该直线的函数表达式;
(3)P是抛物线对称轴上一点,连接PB、PA,是否存在△PAC是直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
 解:(1)∵四边形ABCD是等腰梯形,
解:(1)∵四边形ABCD是等腰梯形,∴OB=
 (AB-CD)=
(AB-CD)= ×(4-2)=1,则 B(-1,0);
×(4-2)=1,则 B(-1,0);∴OA=AB-OB=3,即 A(3,0).
在Rt△OBC中,OC=
 =
= =3,则 C(0,3);
=3,则 C(0,3);设抛物线的解析式为:y=a(x+1)(x-3),代入C点坐标,得:
a(0+1)(0-3)=3,a=-1
∴抛物线的解析式:y=-(x+1)(x-3)=-x2+2x+3.
(2)若以E、A、D、C为顶点的四边形是平行四边形,分两种情况:
①当EC
 AD时,CD=AE=2,OE=OA-AE=1,则E(1,0),如图(2)-①;
AD时,CD=AE=2,OE=OA-AE=1,则E(1,0),如图(2)-①;取平行四边形的对角线交点F,则F(1.5,1.5);
设直线BF的解析式为:y=kx+b,则:
 ,解得
,解得
∴该直线的函数表达式:y=
 x+
x+ ;
;②当AC
 DE,CD=AE=2,OE=OA+AE=5,则E(5,0),如图(2)-②;
DE,CD=AE=2,OE=OA+AE=5,则E(5,0),如图(2)-②;取EC的中点G(2.5,1.5),同①可求得直线BG:y=
 x+
x+ ;
;综上,符合条件的直线有两条,且函数表达式为:y=
 x+
x+ 或y=
或y= x+
x+ .
. (3)假设存在符合条件的P点,分三种情况:
(3)假设存在符合条件的P点,分三种情况:①以点A为直角顶点,AC、AP1为直角边,如右图;
∵OA=OC=3,
∴△OAC是等腰直角三角形,即∠OAC=45°;
∴∠MAP1=45°,即△MAP1也为等腰直角三角形,且MA=MP1=2;
∴P1(1,-2);
②以C为直角顶点,AC、CP2为直角边,如右图;
同①可求得△CP2N、△CHN、△CP2H都是等腰直角三角形,
∴P2H=HN=CH=1,则P2M=3+1=4,即P2(1,4).
③以AC为斜边,AP3、CP3为直角边,如右图;
设点P3(1,m),则:
AP32=(1-3)2+(m-0)2=m2+4、CP32=(1-0)2+(m-3)2=m2-6m+10、AC2=25;
由勾股定理得:AP32+CP32=AC2,即:
m2+4+m2-6m+10=18,化简,得:m2-3m-2=0
解得:m=

∴P3(1,
 )
)综上,存在符合条件的P点,且坐标为:P(1,-2),(1,4),(1,
 ),(1,
),(1, ).
).分析:(1)根据等腰梯形的性质以及AB、CD的线段长,先求出OB以及A、B点的坐标;在Rt△OBC中,BC、OB长已知,由勾股定理可求出OC的长,即可得到点C的坐标;在明确A、B、C三点坐标后,利用待定系数法即可求出该抛物线的解析式.
(2)由于点E在x轴上,若“以E、A、D、C为顶点的四边形是平行四边形”,那么要分两种情况考虑:
①EC
 AD,此时AC为平行四边形的对角线;②AC
AD,此时AC为平行四边形的对角线;②AC ED,此时EC为平行四边形的对角线.
ED,此时EC为平行四边形的对角线.若过B的直线将平行四边形分成面积相等的两部分,那么该直线必过平行四边形对角线的交点,因此取对角线AC或EC的中点,结合B点坐标,即可求出经过这两点的直线的解析式.
(3)若△PAC是直角三角形,那么需要分三种情况考虑:①C为直角顶点、AC作直角边;②A为直角顶点、AC作直角边;③AC为斜边,以P作直角顶点.
点评:该题考查的内容较为复杂,涉及了函数解析式的确定、平行四边形的性质、图形面积的解法、直角三角形的判定、勾股定理的应用等重点知识;后两个小题需要考虑的情况较多,需要牢固掌握相关的基础知识,在解题过程中,要注意数形结合和分类讨论的数学思想.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: