题目内容
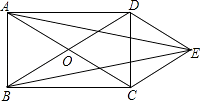
【题目】如图，矩形ABCD的对角线AC、BD相交于点O，DE∥AC，CE∥BD． 
（1）求证：四边形OCED为菱形；
（2）连接AE、BE，AE与BE相等吗？请说明理由．
【答案】
（1）证明：∵DE∥AC，CE∥BD，
∴四边形DOCE是平行四边形，
∵矩形ABCD的对角线AC、BD相交于点O，
∴OC= 
AC= BD=OD，
∴四边形OCED为菱形；
（2）解：AE=BE．
理由：∵四边形OCED为菱形，
∴ED=CE，∴∠EDC=∠ECD，
∴∠ADE=∠BCE，
在△ADE和△BCE中，
，
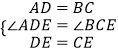∴△ADE≌△BCE（SAS），
∴AE=BE．
【解析】（1）首先利用平行四边形的判定得出四边形DOCE是平行四边形，进而利用矩形的性质得出DO=CO，即可得出答案；（2）利用等腰三角形的性质以及矩形的性质得出AD=BC，∠ADE=∠BCE，进而利用全等三角形的判定得出．
【考点精析】通过灵活运用菱形的判定方法和矩形的性质，掌握任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形；矩形的四个角都是直角，矩形的对角线相等即可以解答此题．
练习册系列答案
相关题目
【题目】小林在某商店购买商品A、B共三次，只有一次购买时，商品A、B同时打折，其余两次均按标价购买，三次购买商品A、B的数量和费用如下表：
购买商品A的数量（个） | 购买商品B的数量（个） | 购买总费用（元） | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
（1）小林以折扣价购买商品A、B是第次购物；
（2）求出商品A、B的标价；
（3）若商品A、B的折扣相同，问商店是打几折出售这两种商品的？
