题目内容
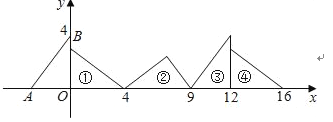
【题目】如图,![]() 为原点,数轴上两点
为原点,数轴上两点![]() 所对应的数分别为
所对应的数分别为![]() ,且
,且![]() 满足关于
满足关于![]() 的整式
的整式![]() 与
与![]() 之和是是单项式,动点
之和是是单项式,动点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() 向终点
向终点![]() 运动.
运动.
(1)求![]() 的值.
的值.
(2)当![]() 时,求点
时,求点![]() 的运动时间
的运动时间![]() 的值.
的值.
(3)当点![]() 开始运动时,点
开始运动时,点![]() 也同时以每秒
也同时以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() 向终点
向终点![]() 运动,若
运动,若![]() ,求
,求![]() 的长.
的长.
【答案】(1) m=-40,n=30.(2)t=5.(3)AP=![]() 或AP=70.
或AP=70.
【解析】
(1)根据单项式的次数相同,列方程即可得到答案;
(2) 分情况讨论:当点P在O的左侧时:当点P在O的右侧时.即可得到答案.
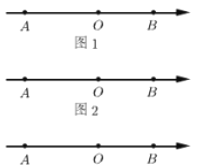
(3)结合题意分别计算:①如图1,当点P在点Q左侧时,如图2,当点P在点Q右侧时.
(1)因为m、n满足关于x、y的整式-x41+myn+60与2xy3n之和是单项式
所以![]()
所以m=-40,n=30.
(2)因为A、B所对应的数分别为-40和30,
所以AB=70,AO=40,BO=30,
当点P在O的左侧时:
则PA+PO=AO=40,
因为PB-(PA+PO)=10,PB=AB-AP=70-4t
所以70-4t-40=10
所以t=5.
当点P在O的右侧时:
因为PB<PA
所以PB-(PA+PO)<0,不合题意,舍去
(3)①如图1,当点P在点Q左侧时,
![]()
因为AP=4t,BQ=2t,AB=70
所以PQ=AB-(AP+BQ)=70-6t
又因为PQ=![]() AB=35
AB=35
所以70-6t=35
所以t=![]() ,AP=
,AP=![]() =
=![]() ,
,
②如图2,当点P在点Q右侧时,
![]()
因为AP=4t,BQ=2t,AB=70,
所以PQ=(AP+BQ)-AB=6t-70,
又因为PQ=![]() AB=35
AB=35
所以6t-70=35
所以t=![]()
所以AP=![]() =70.
=70.

【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备.现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 180 |
(1)求a,b的值;
(2)治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.