题目内容
【题目】如图,已知反比例函数y=kx-1(k>0)的图象与一次函数图象y=﹣x+4交于a、b两点,点a的纵坐标为3.
(1)求反比例函数的解析;
(2)y轴上是否存在一点P,使2∠APB=∠AOB?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(0, ![]() )或(0,-
)或(0,-![]() )
)
【解析】(1)根据A在y=-x+4上,且点A的纵坐标为3,于是得到A(3,1),由于点A在反比例函数![]() 的图象上,即可得到结论;(2)根据勾股定理得到OA=
的图象上,即可得到结论;(2)根据勾股定理得到OA=![]() ,根据2∠APB=∠AOB,于是推出点P在以O为圆心,以OA为半径的圆上,得到OP=
,根据2∠APB=∠AOB,于是推出点P在以O为圆心,以OA为半径的圆上,得到OP=![]() ,即可得到结论.
,即可得到结论.
解:(1)∵A在y=-x+4上,且点A的纵坐标为3,得到A(3,1),
∵点A在反比例函数![]() 的图象上,得k=3,
的图象上,得k=3,
∴反比例函数的解析为: ![]() .
.
(2)如图所示,
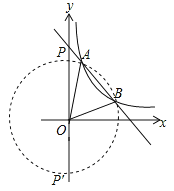
∵A(3,1),∴OA=![]() ,
,
∵2∠APB=∠AOB,
∴点P在以O为圆心,以OA为半径的圆上,
∴OP=![]() ,
,
∵点P在y轴上,
∴P(0, ![]() )或P
)或P![]() (0,
(0, ![]() ).
).
“点睛”本题考查反比例函数的图象与一次函数的交点问题,圆周角定理,勾股定理,正确作出辅助圆是解题关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目



