题目内容
已知如图,梯形ABCD中,AD∥BC,AB=DC,∠BAD、∠CDA的平分线AE、DF分别交直线BC于点E、F。求证:CE=BF。
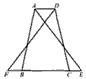
证明:在梯形ABCD中,AB=DC,
∴∠ABC=∠DCB,∠BAD=∠CDA
∵AE.DF分别为∠BAD与∠CDA的平分线,
∴∠BAE=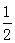 ∠BAD,∠CDF=
∠BAD,∠CDF=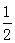 ∠CDA,
∠CDA,
∴∠BAE=∠CDF
∴△ABE≌△DCF
∴BE=CF
∴BE-BC=CF-BC,即BF=CE。
∴∠ABC=∠DCB,∠BAD=∠CDA
∵AE.DF分别为∠BAD与∠CDA的平分线,
∴∠BAE=
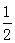 ∠BAD,∠CDF=
∠BAD,∠CDF=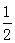 ∠CDA,
∠CDA,∴∠BAE=∠CDF
∴△ABE≌△DCF
∴BE=CF
∴BE-BC=CF-BC,即BF=CE。

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 (2012•通州区一模)已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE.
(2012•通州区一模)已知如图,在△ABC中,AB=AC,∠ABC=α,将△ABC以点B为中心,沿逆时针方向旋转α度(0°<α<90°),得到△BDE,点B、A、E恰好在同一条直线上,连接CE.


 ,请你求出四边形DBCE的面积.
,请你求出四边形DBCE的面积.
 ,请你求出四边形DBCE的面积.
,请你求出四边形DBCE的面积.