题目内容
【题目】如图,抛物线的顶点D的坐标为(1,﹣4),与y轴交于点C(0,﹣3),与x轴交于A、B两点.
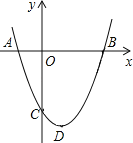
(1)求该抛物线的函数关系式;
(2)在抛物线上存在点P(不与点D重合),使得S△PAB=S△ABD,请求出P点的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)点P的坐标为(1+2![]() ,4)或(1﹣2
,4)或(1﹣2![]() ,4).
,4).
【解析】
试题分析:(1)由抛物线的顶点D的坐标为(1,﹣4),可设抛物线的函数关系式为y=a(x﹣1)2﹣4,再将C(0,﹣3)代入求解即可;
(2)由S△PAB=S△ABD,根据三角形面积公式可得点P到线段AB的距离一定等于顶点D到AB的距离,而D的坐标为(1,﹣4),所以点P的纵坐标一定为4.将y=4代入(1)中所求解析式,得到x2﹣2x﹣3=4,解方程求出x的值,进而得到点P的坐标.
解:(1)∵抛物线的顶点D的坐标为(1,﹣4),
∴设抛物线的函数关系式为y=a(x﹣1)2﹣4,
又∵抛物线过点C(0,﹣3),
∴﹣3=a(0﹣1)2﹣4,
解得a=1,
∴抛物线的函数关系式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3;
(2)∵S△PAB=S△ABD,且点P在抛物线上,
∴点P到线段AB的距离一定等于顶点D到AB的距离,
∴点P的纵坐标一定为4.
令y=4,则x2﹣2x﹣3=4,
解得x1=1+2![]() ,x2=1﹣2
,x2=1﹣2![]() .
.
∴点P的坐标为(1+2![]() ,4)或(1﹣2
,4)或(1﹣2![]() ,4).
,4).

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目