��Ŀ����
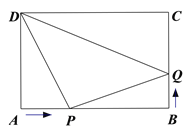
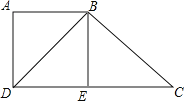
����Ŀ����ͼ����ABC�ı�AB�ǡ�O��ֱ������C�ڡ�O�ϣ���֪AC��6cm��BC��8cm����P��Q�ֱ��ڱ�AB��BC�ϣ��ҵ�P�����A��B�غϣ�BQ��kAP��k��0��������PC��PQ��
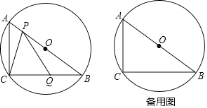
��1�����O�İ뾶����
��2����k��2ʱ����AP��x����CPQ�����Ϊy����y����x�ĺ�����ϵʽ����д��������
��3�������CPQ����ABC���ƣ��ҡ�ACB����CPQ����k��ֵ��
���𰸡���1��5����2��y=![]() ;��3��
;��3��![]()
��������
��1������֤����ACB��90����Ȼ�����ù��ɶ������ɽ�����⣻
��2����ͼ2�У���PH��BC��H����PH��AC�����Ƴ�![]() ���Ƴ�
���Ƴ�![]() ���ó�
���ó�![]() ������
������![]() ���㼴�ɣ�
���㼴�ɣ�
��3����Ϊ��CPQ����ABC���ƣ���CPQ����ACB��90��������Ϊ��CQP����B��
����ֻ�С�PCB����B���Ƴ�PC��PB���ɡ�B+��A��90������ACP+��PCB��90����
�Ƴ���A����ACP���ó�PA��PC��PB��5���ɡ�COQ�ס�BCA���Ƴ�![]() ��
��
�Ƴ�![]() �����ɽ������.
�����ɽ������.
��1����AB��ֱ����
���ACB��90������AC��6��BC��8��
��![]() ��
��
���O�İ뾶Ϊ5��
��2����ͼ2�У���PH��BC��H��

��PH��AC��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��3����ͼ2�У�

�ߡ�CPQ����ABC���ƣ���CPQ����ACB��90����
�֡ߡ�CQP����B��
��ֻ�С�PCB����B��
��PC��PB��
�ߡ�B+��A��90������ACP+��PCB��90����
���A����ACP��
��PA��PC��PB��5��
���COQ�ס�BCA��
��![]() ��
��
��![]() ��
��
��![]() ��
��

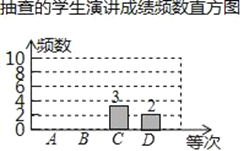
����Ŀ��ijУΪ��ף�����������������2018��4�µ���֯��Уѧ���ٰ������������ľ�����г�����������ݽ�������Ϊ�˽�ѧ�����ݽ������еijɼ������ѧУ�����ȡ�˲���ѧ�����ݽ������ɼ�����ͳ��(���֣�100�֣��ȴΣ�A�����㣺90��100�֣�B�����ã�80��89�֣�C��һ�㣺60��79�֣�D���ϲ60�����£�����60��)�õ����²�������ͼ����
�ȴ� | Ƶ�� | Ƶ�� |
A | a | 0.25 |
B | b | 0.5 |
C | 3 | m |
D | 2 | 0.1 |
����������Ϣ�����������
(1)����a��_____��b��_____��m��_______������ȫƵ���ֲ�ֱ��ͼ��
(2)���ݳ��ѧ���ݽ��ɼ�Ƶ��ͳ�Ʊ�����������ͳ��ͼ�У���ʾC�ȴβ��ֵ��������ĽǵĶ�����_______��
(3)��A�ȴ�����2��Ů��������Ϊ������ѧУ����A�ȴ�ѧ���г�ȡ2��ѧ������ݽ���ϲμ�ȫ�����������걭���ݽ���������ǡ�ó�ȡ1��������1��Ů���ĸ��ʣ�